Chapter 26 [fMRI] NPS ~ singletrial | A Minimal Book Example

What is the purpose of this notebook?

Here, I model NPS dot products as a function of cue, stimulus intensity and expectation ratings.
One of the findings is that low cues lead to higher NPS dotproducts in the high intensity group, and that this effect becomes non-significant across sessions.
03/23/2023: For now, I’m grabbing participants that have complete data, i.e. 18 runs, all three sessions.

Contrast weight table

Table 26.1: Contrast weights
	pain	vicarious	cognitive
task_V_gt_C	0.00	0.50	-0.50
task_P_gt_VC	0.66	-0.34	-0.34

26.1 NPS ~ paintask: 2 cue x 3 stimulus_intensity

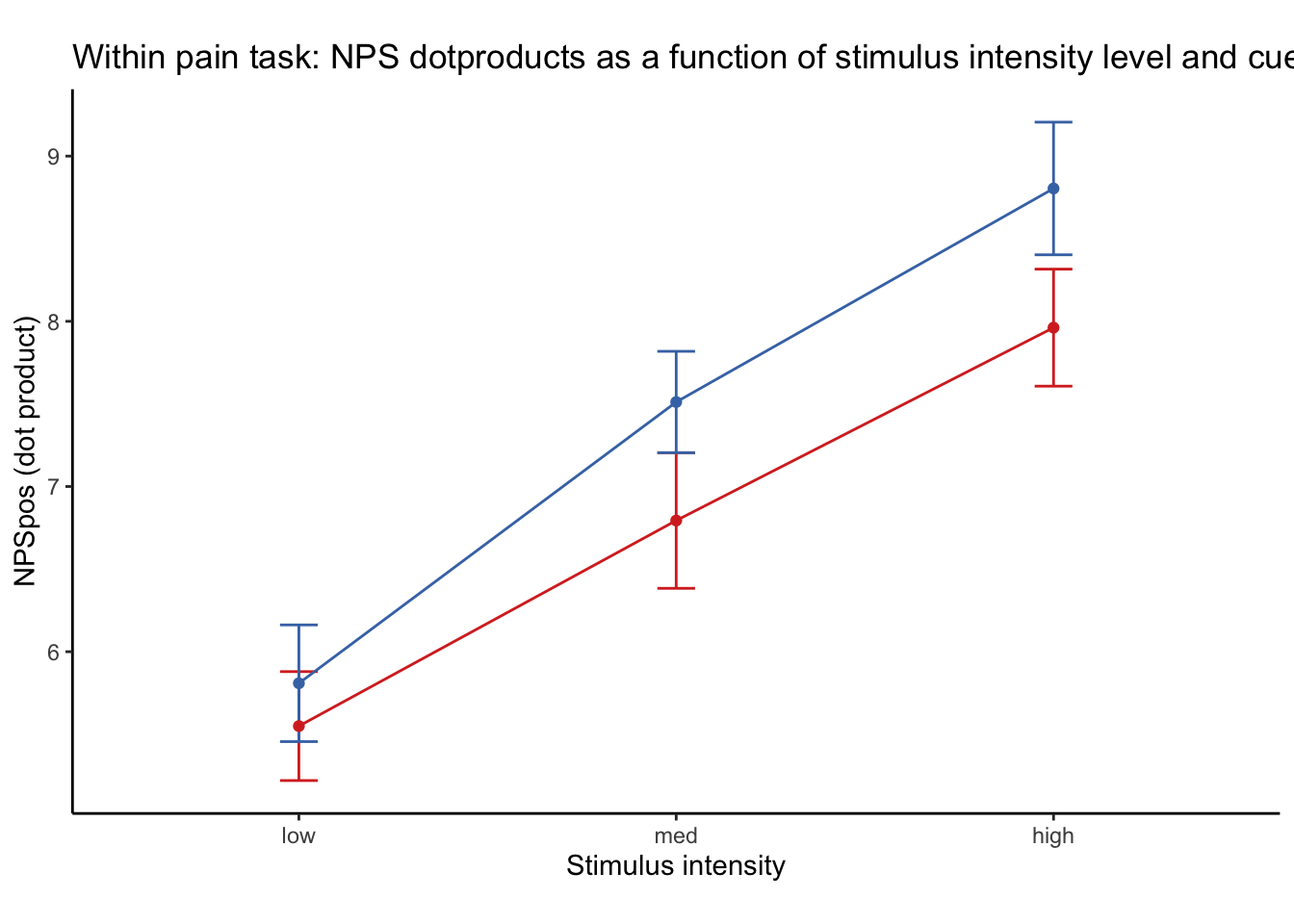
Q. Within pain task, Does stimulus intenisty level and cue level significantly predict NPS dotproducts?

Lineplots

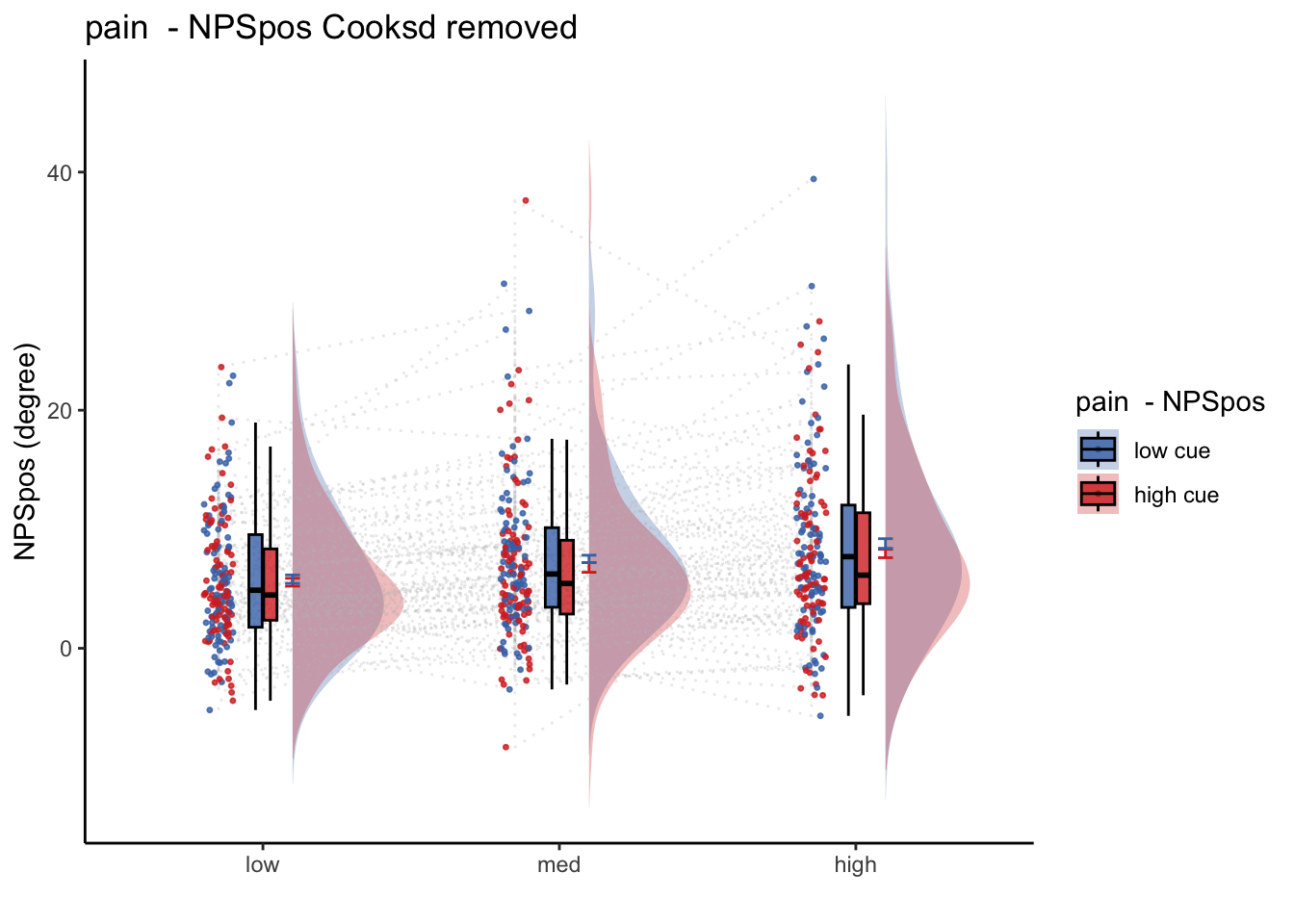
26.1.1 Linear model results (NPS ~ paintask: 2 cue x 3 stimulus_intensity)

model.npscuestim <- lmer(NPSpos ~ 
                          CUE_high_gt_low*STIM_linear +CUE_high_gt_low * STIM_quadratic +
                          (CUE_high_gt_low+STIM|sub), data = data_screen
                    )
sjPlot::tab_model(model.npscuestim,
                  title = "Multilevel-modeling: \nlmer(NPSpos ~ CUE * STIM + (CUE + STIM | sub), data = pvc)",
                  CSS = list(css.table = '+font-size: 12;'))

Multilevel-modeling: lmer(NPSpos ~ CUE * STIM + (CUE + STIM | sub), data = pvc)
	NPSpos
Predictors	Estimates	CI	p
(Intercept)	7.01	5.85 – 8.17	<0.001
CUE high gt low	-0.77	-1.31 – -0.23	0.005
STIM linear	2.62	1.93 – 3.31	<0.001
STIM quadratic	0.02	-0.53 – 0.57	0.944
CUE high gt low * STIM linear	-0.62	-1.83 – 0.59	0.311
CUE high gt low * STIM quadratic	-0.67	-1.73 – 0.39	0.214
Random Effects
σ²	62.90
τ₀₀ _sub	39.93
τ₁₁ _{sub.CUE_high_gt_low}	0.96
τ₁₁ _sub.STIMlow	2.45
τ₁₁ _sub.STIMmed	1.81
ρ₀₁	-0.61
	-0.96
	-0.82
N _sub	91
Observations	3961
Marginal R² / Conditional R²	0.021 / NA

Linear model eta-squared

Parameter	Eta2_partial	CI	CI_low	CI_high
CUE_high_gt_low	0.0659453	0.95	0.0109806	1
STIM_linear	0.2695449	0.95	0.1750191	1
STIM_quadratic	0.0000189	0.95	0.0000000	1
CUE_high_gt_low:STIM_linear	0.0002695	0.95	0.0000000	1
CUE_high_gt_low:STIM_quadratic	0.0004054	0.95	0.0000000	1

Linear model Cohen’s d: NPS stimulus_intensity d = 1.16, cue d = 0.45

	t	df	d
CUE_high_gt_low	-2.784759	109.8409	-0.5314172
STIM_linear	7.450178	150.4166	1.2149230
STIM_quadratic	0.069956	259.5231	0.0086849
CUE_high_gt_low:STIM_linear	-1.012647	3804.3322	-0.0328359
CUE_high_gt_low:STIM_quadratic	-1.241596	3800.8213	-0.0402783

26.1.2 2 cue * 3 stimulus_intensity * expectation_rating

data_screen$EXPECT <- data_screen$event02_expect_angle
model.nps3factor <- lmer(NPSpos ~ 
                          CUE_high_gt_low*STIM_linear*EXPECT +
                           CUE_high_gt_low*STIM_quadratic*EXPECT +
                          (CUE_high_gt_low  |sub), data = data_screen
                    )
sjPlot::tab_model(model.nps3factor,
                  title = "Multilevel-modeling: \nlmer(NPSpos ~ CUE * STIM * EXPECTATION + (CUE + STIM + EXPECT | sub), data = pvc)",
                  CSS = list(css.table = '+font-size: 12;'))

Multilevel-modeling: lmer(NPSpos ~ CUE * STIM * EXPECTATION + (CUE + STIM + EXPECT | sub), data = pvc)
	NPSpos
Predictors	Estimates	CI	p
(Intercept)	6.84	5.49 – 8.20	<0.001
CUE high gt low	-0.72	-1.91 – 0.47	0.238
STIM linear	0.94	-0.37 – 2.25	0.162
EXPECT	0.00	-0.01 – 0.01	0.568
STIM quadratic	0.81	-0.35 – 1.97	0.169
CUE high gt low * STIM linear	-2.58	-5.20 – 0.04	0.054
CUE high gt low * EXPECT	-0.00	-0.02 – 0.01	0.756
STIM linear * EXPECT	0.02	0.01 – 0.04	0.010
CUE high gt low * STIM quadratic	-1.45	-3.76 – 0.87	0.221
EXPECT * STIM quadratic	-0.01	-0.03 – 0.00	0.073
(CUE high gt low * STIM linear) * EXPECT	0.02	-0.02 – 0.05	0.347
(CUE high gt low EXPECT) STIM quadratic	0.02	-0.01 – 0.05	0.262
Random Effects
σ²	63.44
τ₀₀ _sub	29.71
τ₁₁ _{sub.CUE_high_gt_low}	1.04
ρ₀₁ _sub	-0.54
ICC	0.32
N _sub	91
Observations	3825
Marginal R² / Conditional R²	0.016 / 0.332

eta squared

Parameter	Eta2_partial	CI	CI_low	CI_high
CUE_high_gt_low	0.0068023	0.95	0.0000000	1
STIM_linear	0.0005305	0.95	0.0000000	1
EXPECT	0.0001752	0.95	0.0000000	1
STIM_quadratic	0.0005122	0.95	0.0000000	1
CUE_high_gt_low:STIM_linear	0.0010053	0.95	0.0000000	1
CUE_high_gt_low:EXPECT	0.0003779	0.95	0.0000000	1
STIM_linear:EXPECT	0.0017799	0.95	0.0002284	1
CUE_high_gt_low:STIM_quadratic	0.0004069	0.95	0.0000000	1
EXPECT:STIM_quadratic	0.0008710	0.95	0.0000000	1
CUE_high_gt_low:STIM_linear:EXPECT	0.0002392	0.95	0.0000000	1
CUE_high_gt_low:EXPECT:STIM_quadratic	0.0003407	0.95	0.0000000	1

Cohen’s d

	t	df	d
CUE_high_gt_low	-1.1813078	203.7533	-0.1655163
STIM_linear	1.4000859	3692.9301	0.0460786
EXPECT	0.5713317	1863.1849	0.0264722
STIM_quadratic	1.3759005	3693.7820	0.0452774
CUE_high_gt_low:STIM_linear	-1.9278539	3693.3372	-0.0634446
CUE_high_gt_low:EXPECT	-0.3105411	255.1123	-0.0388851
STIM_linear:EXPECT	2.5669934	3695.6467	0.0844519
CUE_high_gt_low:STIM_quadratic	-1.2250398	3686.6417	-0.0403520
EXPECT:STIM_quadratic	-1.7951705	3696.5488	-0.0590524
CUE_high_gt_low:STIM_linear:EXPECT	0.9398663	3692.7896	0.0309328
CUE_high_gt_low:EXPECT:STIM_quadratic	1.1210823	3687.8486	0.0369216

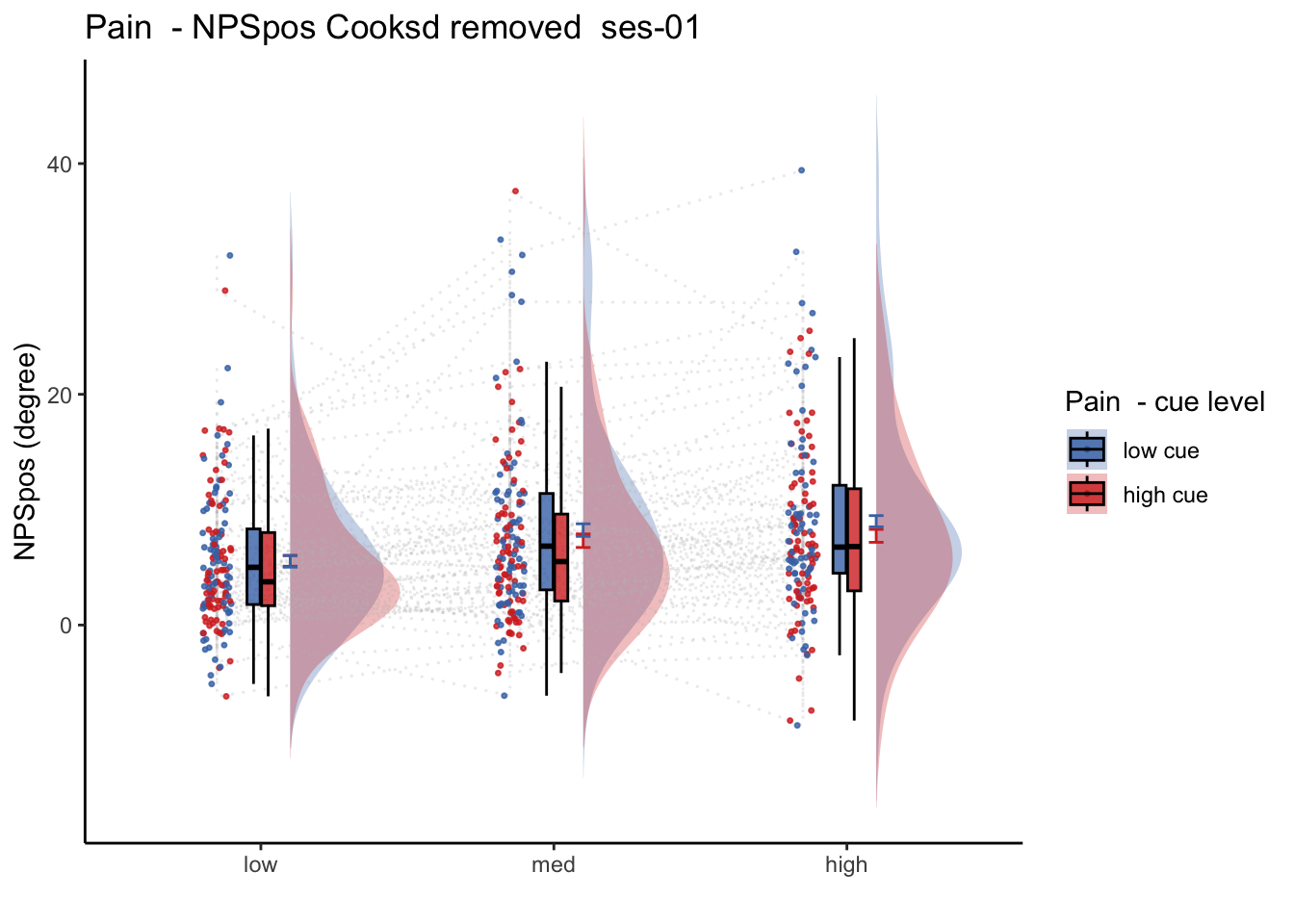
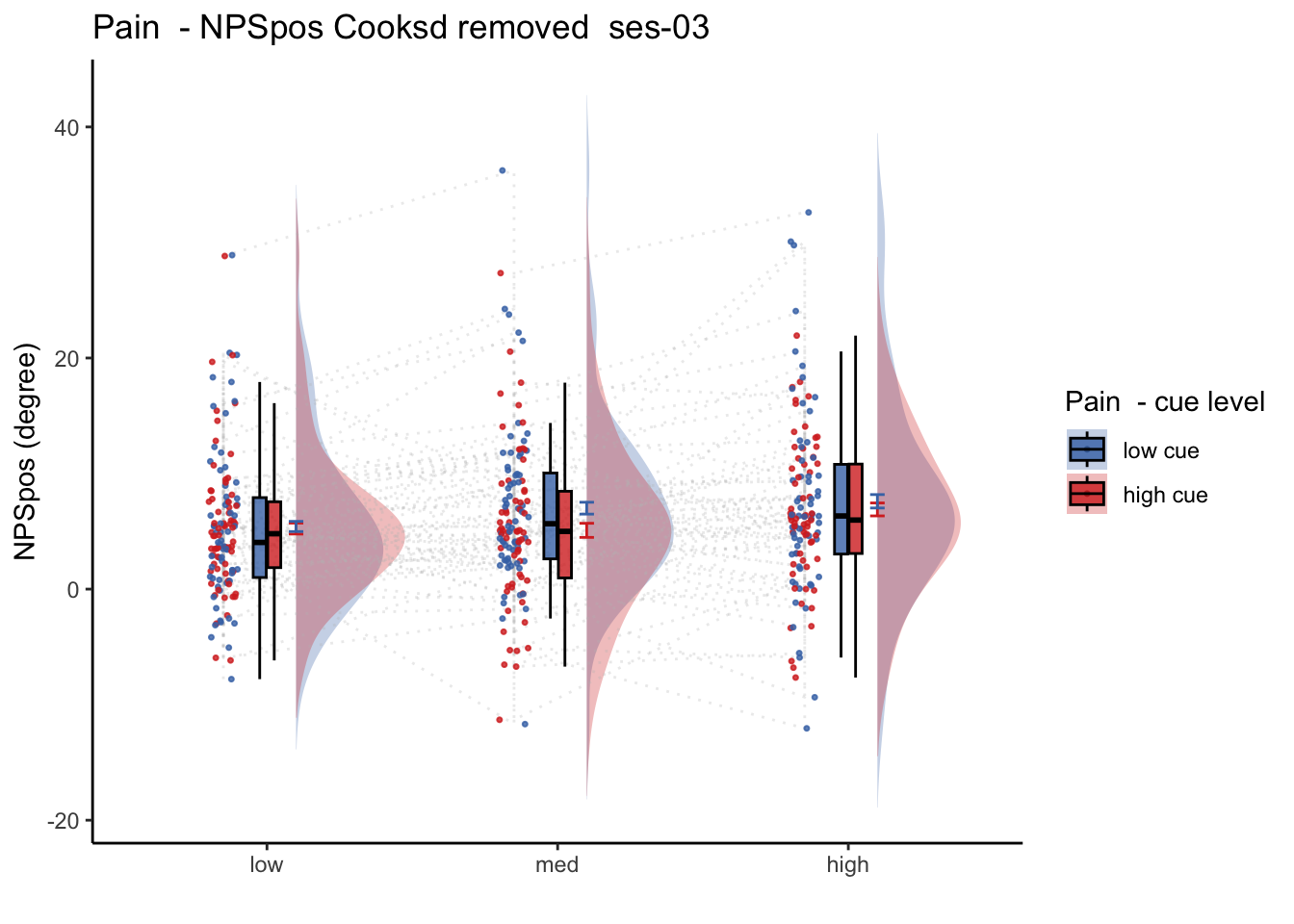
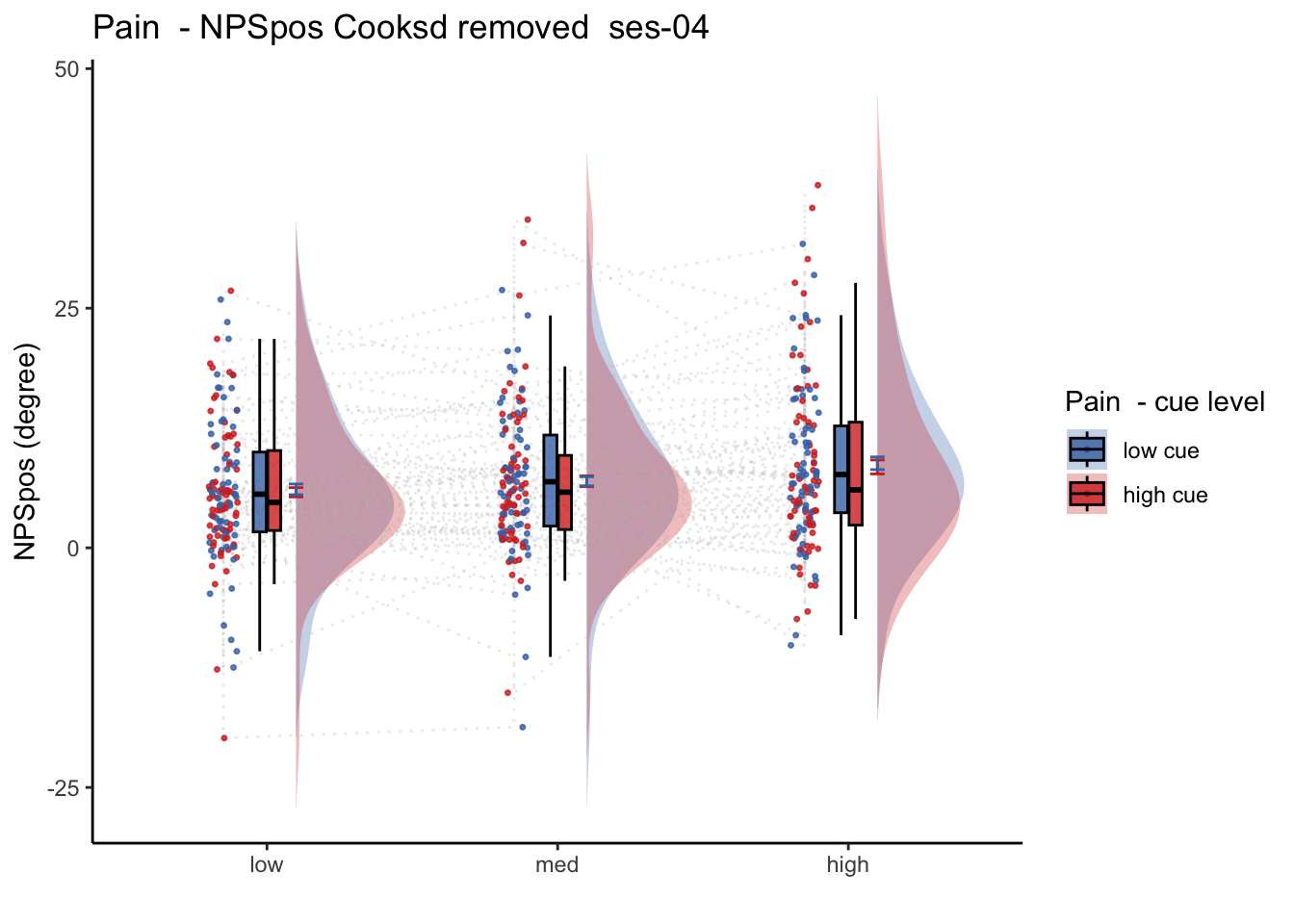
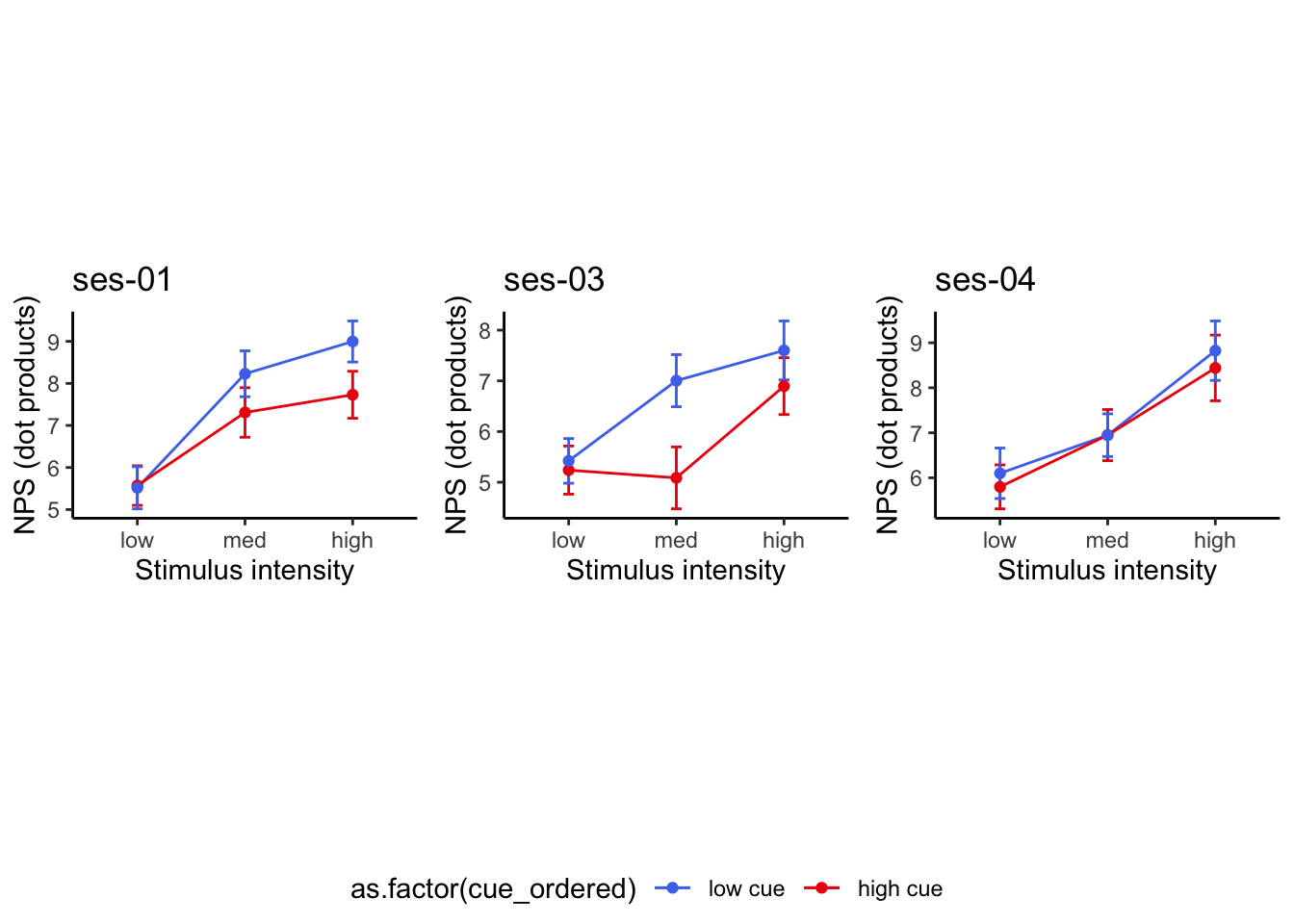
26.2 NPS_ses01 ~ SES * CUE * STIM

Q. Is the cue effect on NPS different across sessions?

Quick answer: Yes, the cue effect in session 1 (for high intensity group) is significantly different; whereas this different becomes non significant in session 4. To unpack, a participant was informed to experience a low stimulus intensity, when in fact they were delivered a high intensity stimulus. This violation presumably leads to a higher NPS response, given that they were delivered a much painful stimulus than expected. The fact that the cue effect is almost non significant during the last session indicates that the cue effects are not just an anchoring effect.

26.2.0.1 Session wise plots

26.2.1 Here are the stats models: NPS~session * cue * stimulus_intensity

Calculate difference score

average high and low cue within run.
calculate difference between high and low cue per run
each participant has 6 contrast scores
run this as a function of stimulus intensity and sessions

26.3 26.4 OUTCOME ~ NPS

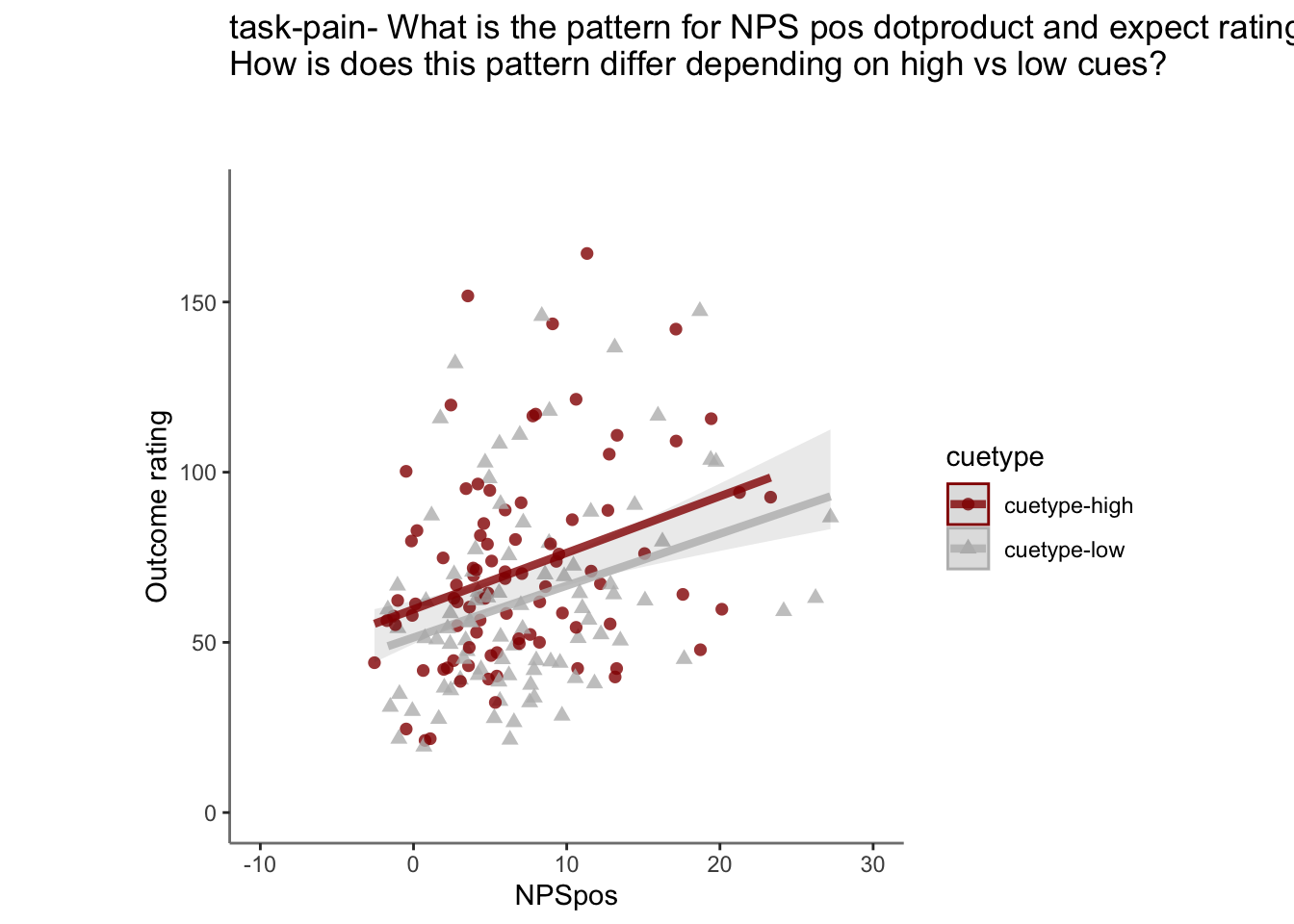
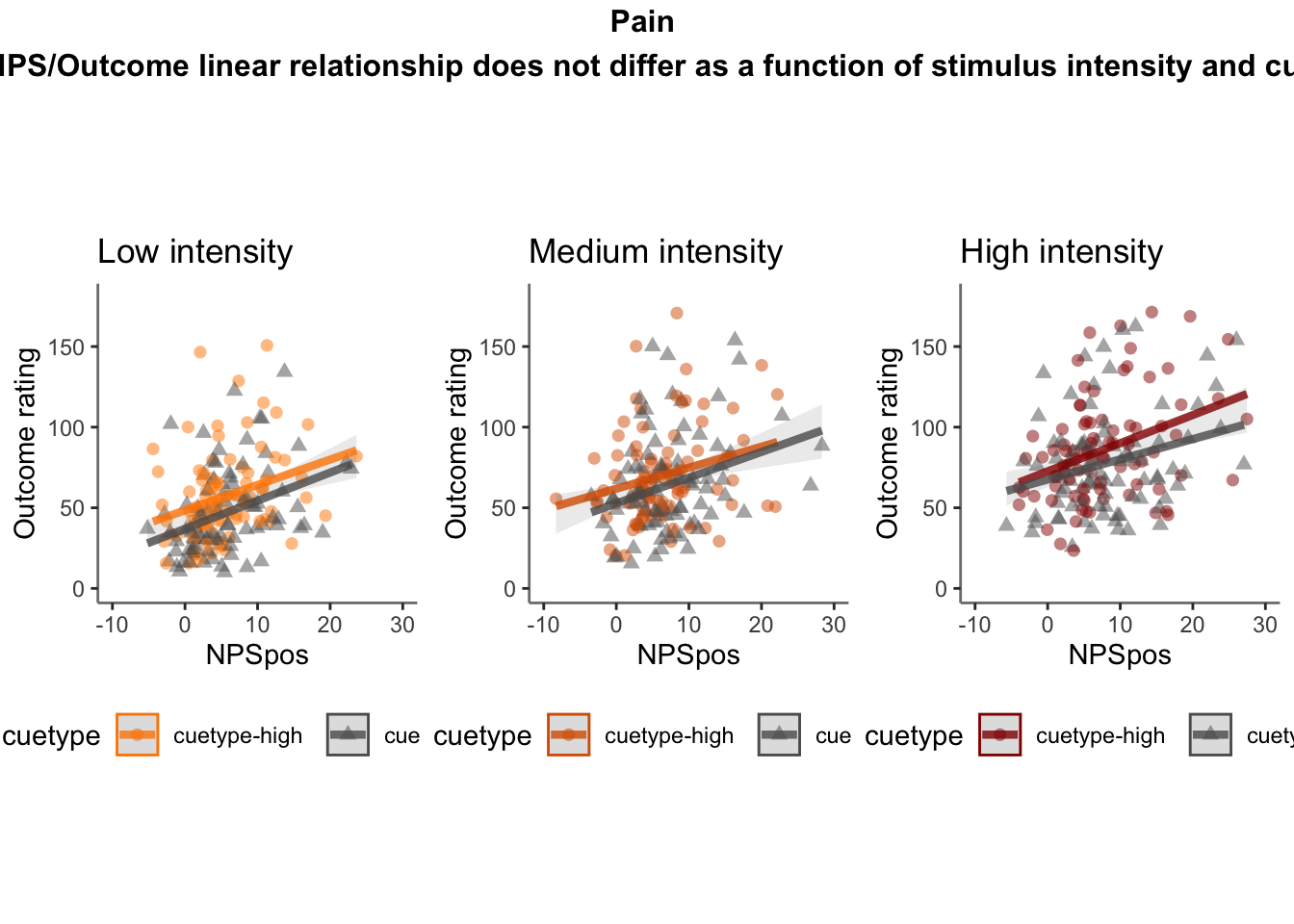
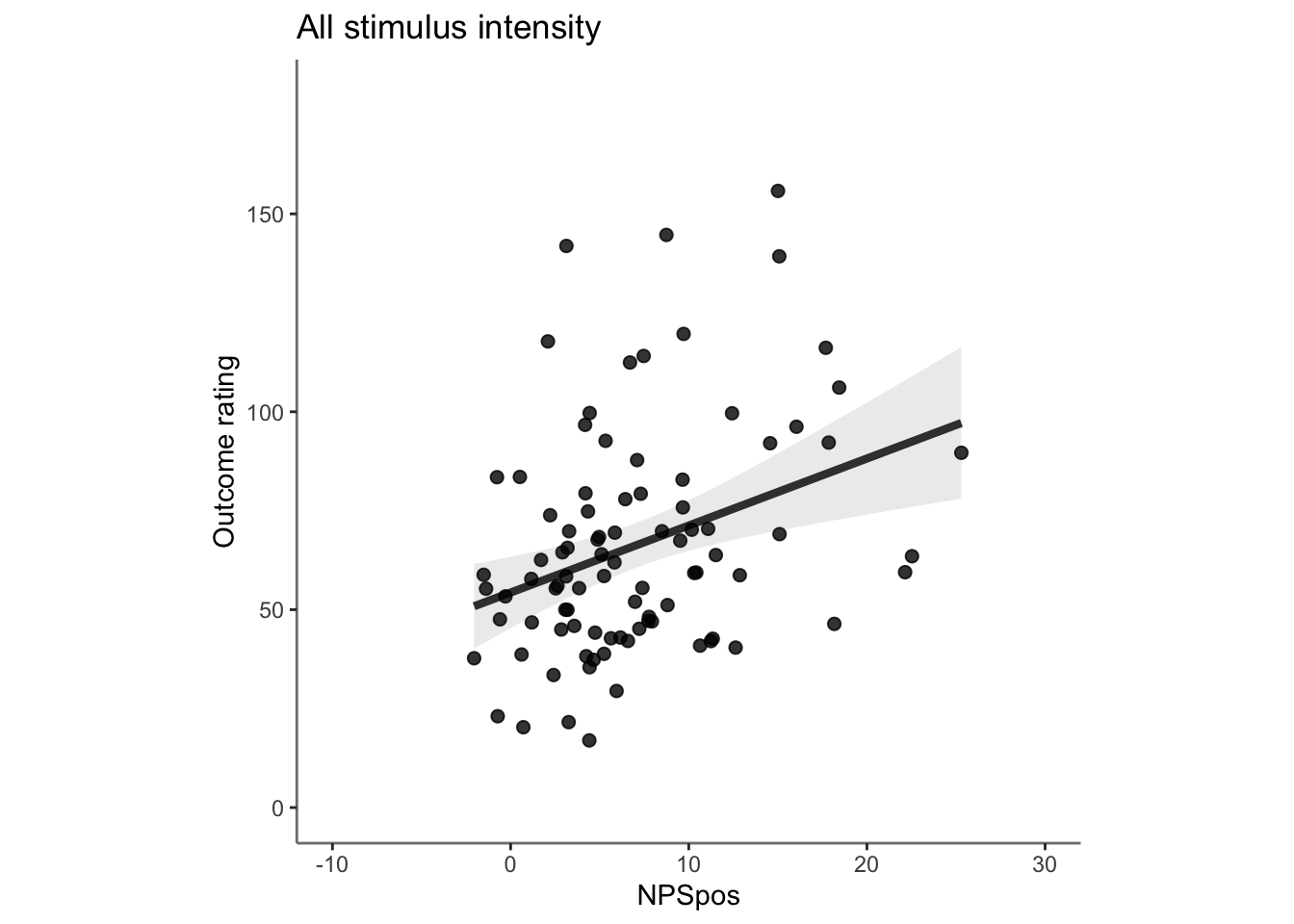
Q. Do higher NPS values indicate higher outcome ratings? (Pain task only)

Yes, Higher NPS values are associated with higher outcome ratings. The linear relationship between NPS value and outcome ratings are stronger for conditions where cue level is congruent with stimulus intensity levels. In other words, NPS-outcome rating relationship is stringent in the low cue-low intensity group, as is the case for high cue-ghigh intensity group.

26.4.1 outcome_rating * cue

26.4.2 outcome_ratings * stimulus_intensity * cue

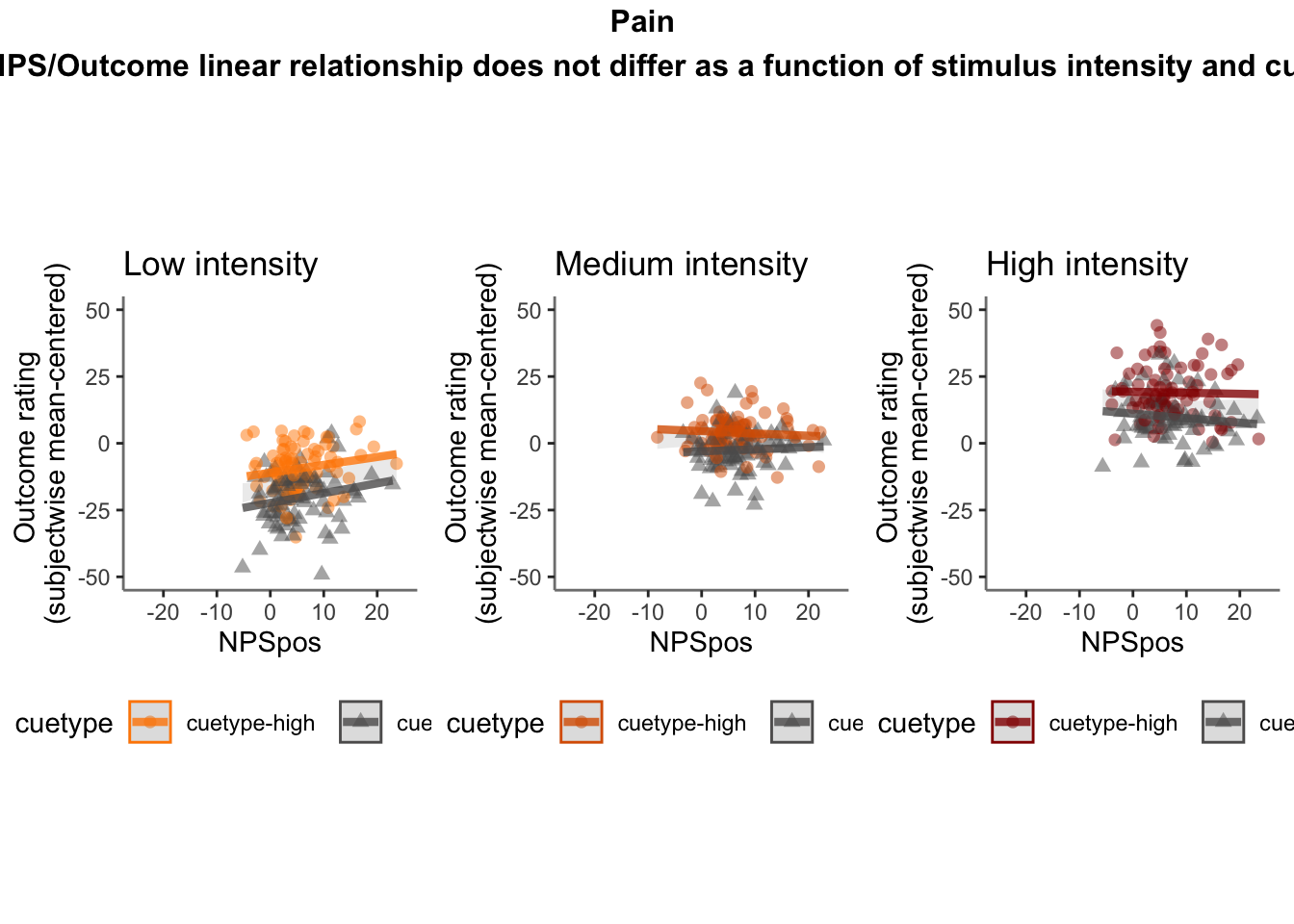
26.4.3 demeaned outcome rating * cue

## `geom_smooth()` using formula = 'y ~ x'

## Warning: Removed 90 rows containing non-finite values (`stat_smooth()`).

## `geom_smooth()` using formula = 'y ~ x'

## Warning: Removed 90 rows containing non-finite values (`stat_smooth()`).

## Warning: Removed 90 rows containing missing values (`geom_point()`).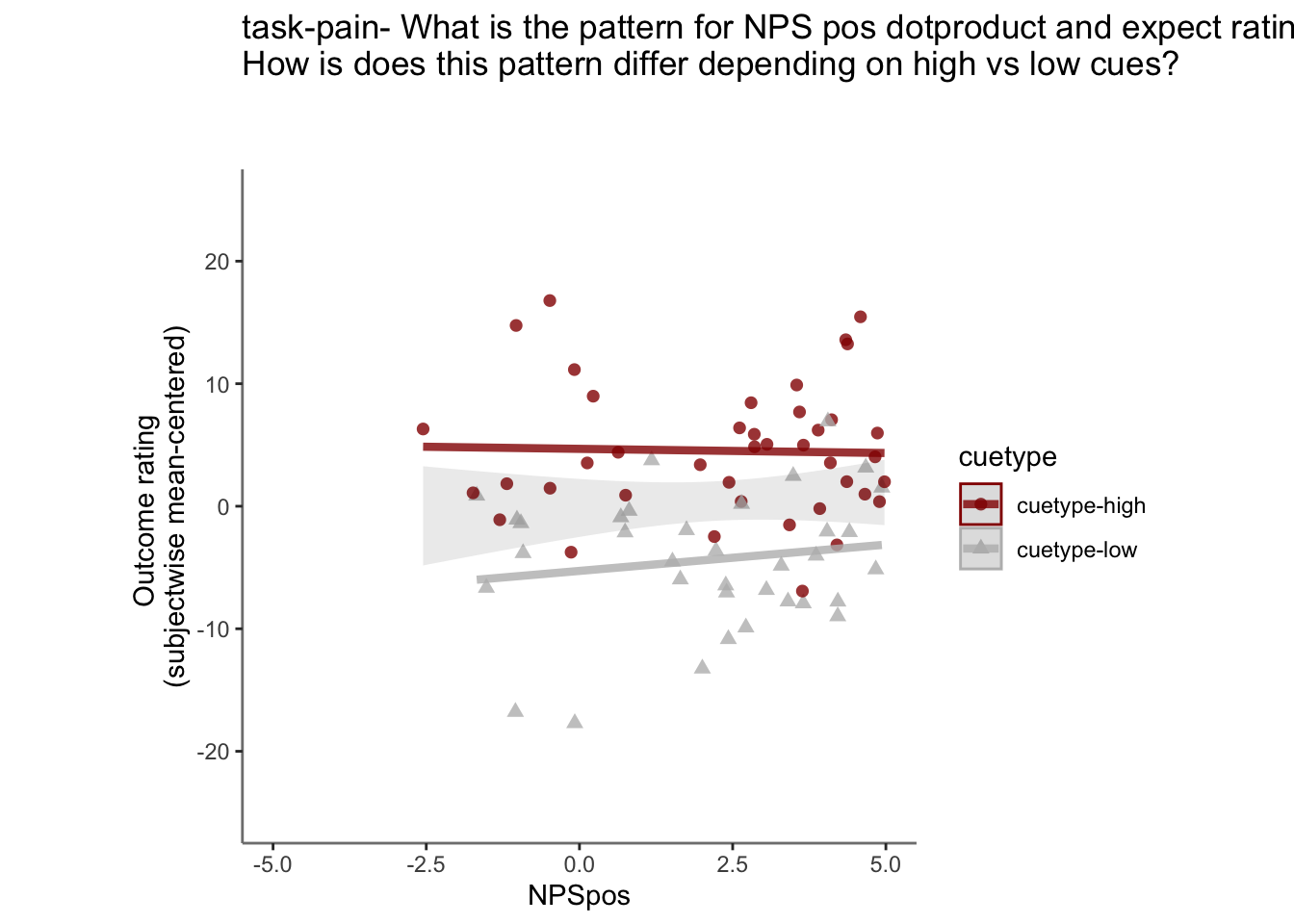

26.4.4 demeaned_outcome_ratings * stimulus_intensity * cue

26.4.5 Is this statistically significant?

# organize variable names
# NPS_demean vs. NPSpos
model.npsoutcome <- lmer(OUTCOME_demean ~ CUE_high_gt_low*STIM_linear*NPSpos + CUE_high_gt_low*STIM_quadratic*NPSpos + (CUE_high_gt_low*STIM*NPSpos|sub), data = demean_dropna)

## Warning: Model failed to converge with 1 negative eigenvalue: -3.2e+02

sjPlot::tab_model(model.npsoutcome,
                  title = "Multilevel-modeling: \nlmer(OUTCOME_demean ~ CUE * STIM * NPSpos + (CUE * STIM *NPSpos | sub), data = pvc)",
                  CSS = list(css.table = '+font-size: 12;'))

Multilevel-modeling: lmer(OUTCOME_demean ~ CUE * STIM * NPSpos + (CUE * STIM *NPSpos | sub), data = pvc)
	OUTCOME_demean
Predictors	Estimates	CI	p
(Intercept)	-1.05	-1.83 – -0.26	0.009
CUE high gt low	9.28	7.05 – 11.50	<0.001
STIM linear	30.72	27.34 – 34.10	<0.001
NPSpos	0.18	0.10 – 0.25	<0.001
STIM quadratic	1.13	-0.55 – 2.81	0.186
CUE high gt low * STIM linear	-2.89	-6.79 – 1.01	0.146
CUE high gt low * NPSpos	-0.06	-0.22 – 0.09	0.409
STIM linear * NPSpos	-0.29	-0.47 – -0.10	0.003
CUE high gt low * STIM quadratic	-3.88	-7.25 – -0.52	0.024
NPSpos * STIM quadratic	-0.01	-0.17 – 0.14	0.875
(CUE high gt low * STIM linear) * NPSpos	0.21	-0.14 – 0.56	0.238
(CUE high gt low NPSpos) STIM quadratic	-0.06	-0.38 – 0.27	0.738
Random Effects
σ²	382.45
τ₀₀ _sub	47.47
τ₁₁ _{sub.CUE_high_gt_low}	89.82
τ₁₁ _sub.STIMlow	155.24
τ₁₁ _sub.STIMmed	44.98
τ₁₁ _sub.NPSpos	0.02
τ₁₁ _{sub.CUE_high_gt_low:STIMlow}	21.43
τ₁₁ _{sub.CUE_high_gt_low:STIMmed}	22.96
τ₁₁ _{sub.CUE_high_gt_low:NPSpos}	0.25
τ₁₁ _{sub.STIMlow:NPSpos}	0.03
τ₁₁ _{sub.STIMmed:NPSpos}	0.06
τ₁₁ _{sub.CUE_high_gt_low:STIMlow:NPSpos}	0.18
τ₁₁ _{sub.CUE_high_gt_low:STIMmed:NPSpos}	0.44
ρ₀₁	-0.15
	-1.00
	-0.99
	-0.98
	0.54
	0.47
	0.62
	0.34
	0.37
	-0.37
	-0.72
N _sub	84
Observations	3839
Marginal R² / Conditional R²	0.305 / NA

26.5 NPS ~ expectation_rating

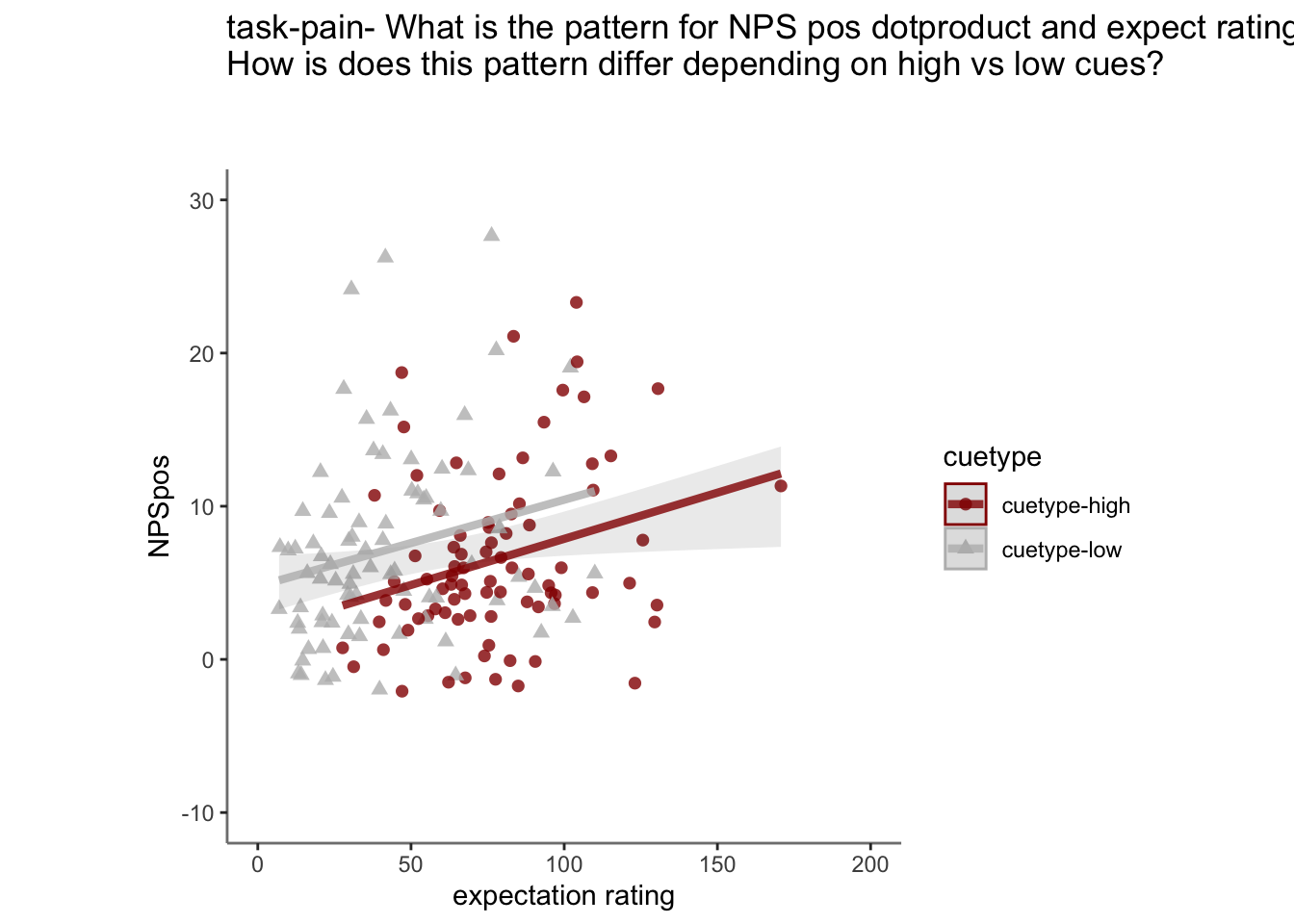
Q. What is the relationship betweeen expectation ratings & NPS? (Pain task only)

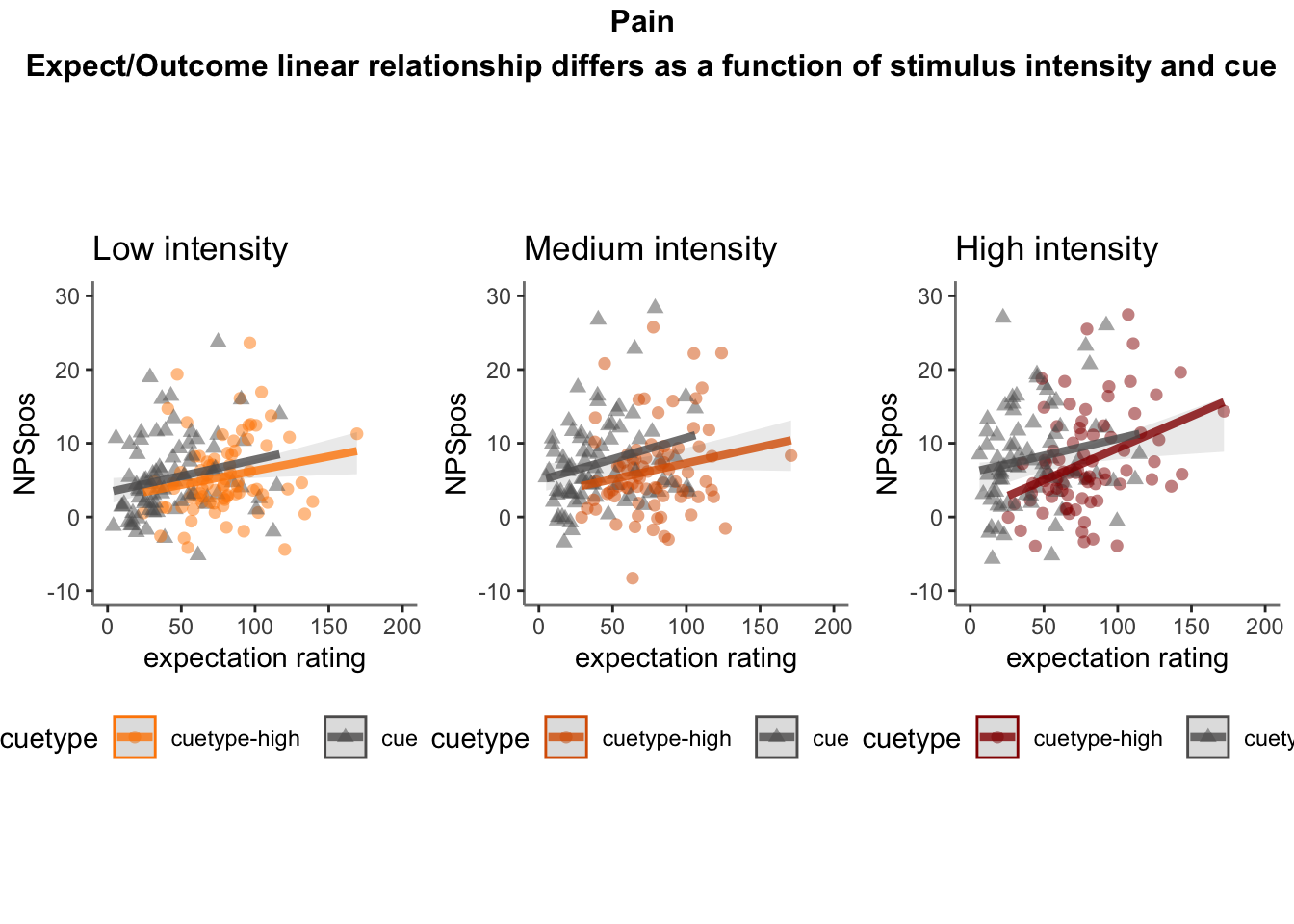
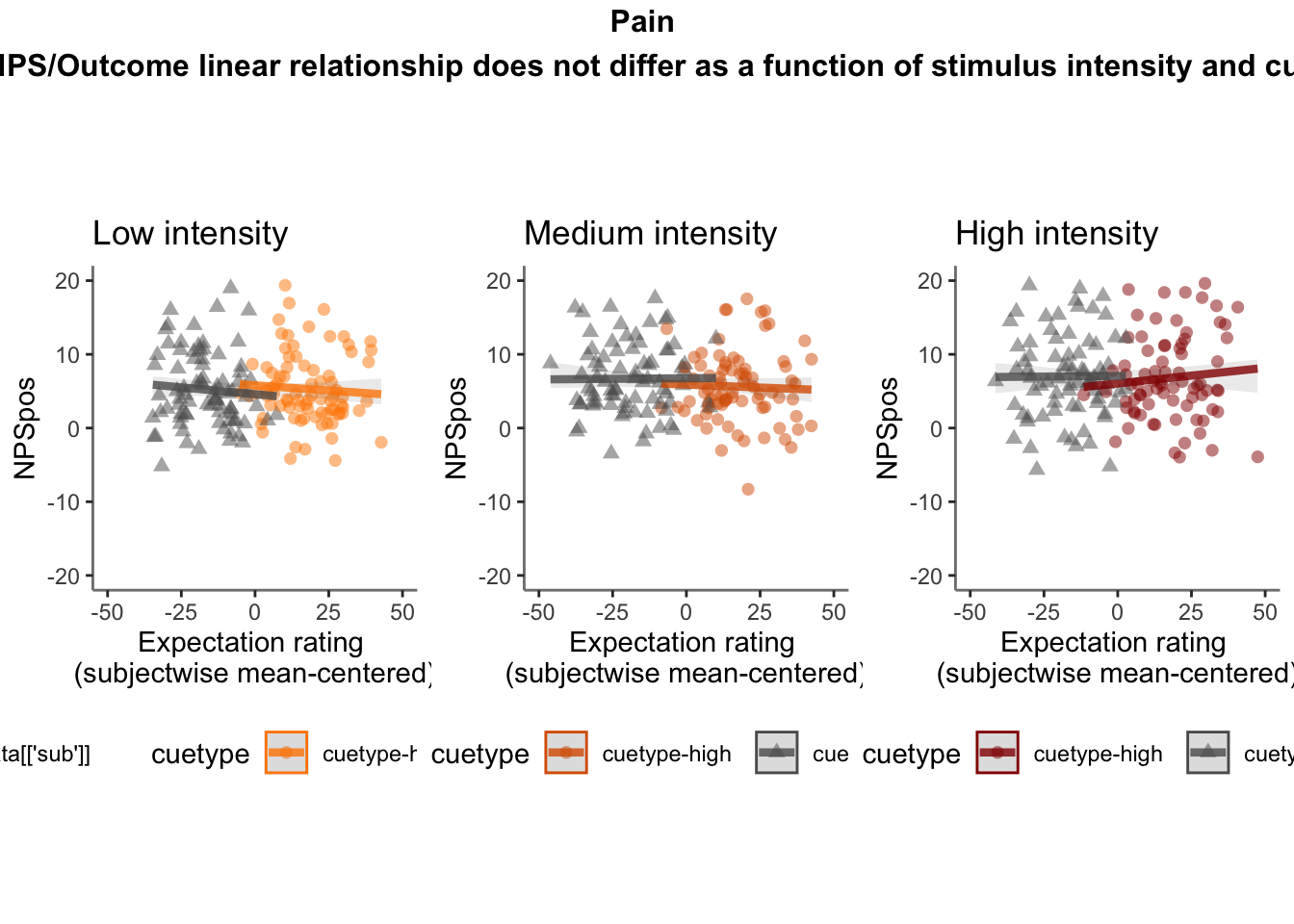
Do we see a linear effect between expectation rating and NPS dot products? Also, does this effect differ as a function of cue and stimulus intensity ratings, as is the case for behavioral ratings?

Quick answer: Yes, expectation ratings predict NPS dotproducts; Also, there tends to be a different relationship depending on cues, just by looking at the figures, although this needs to be tested statistically.

26.5.1 NPS ~ expect * cue

26.5.2 NPS ~ expect * cue * stim

26.5.3 NPS ~ demeaned_expect * cue

26.5.4 NPS ~ demeaned_expect * cue * stim

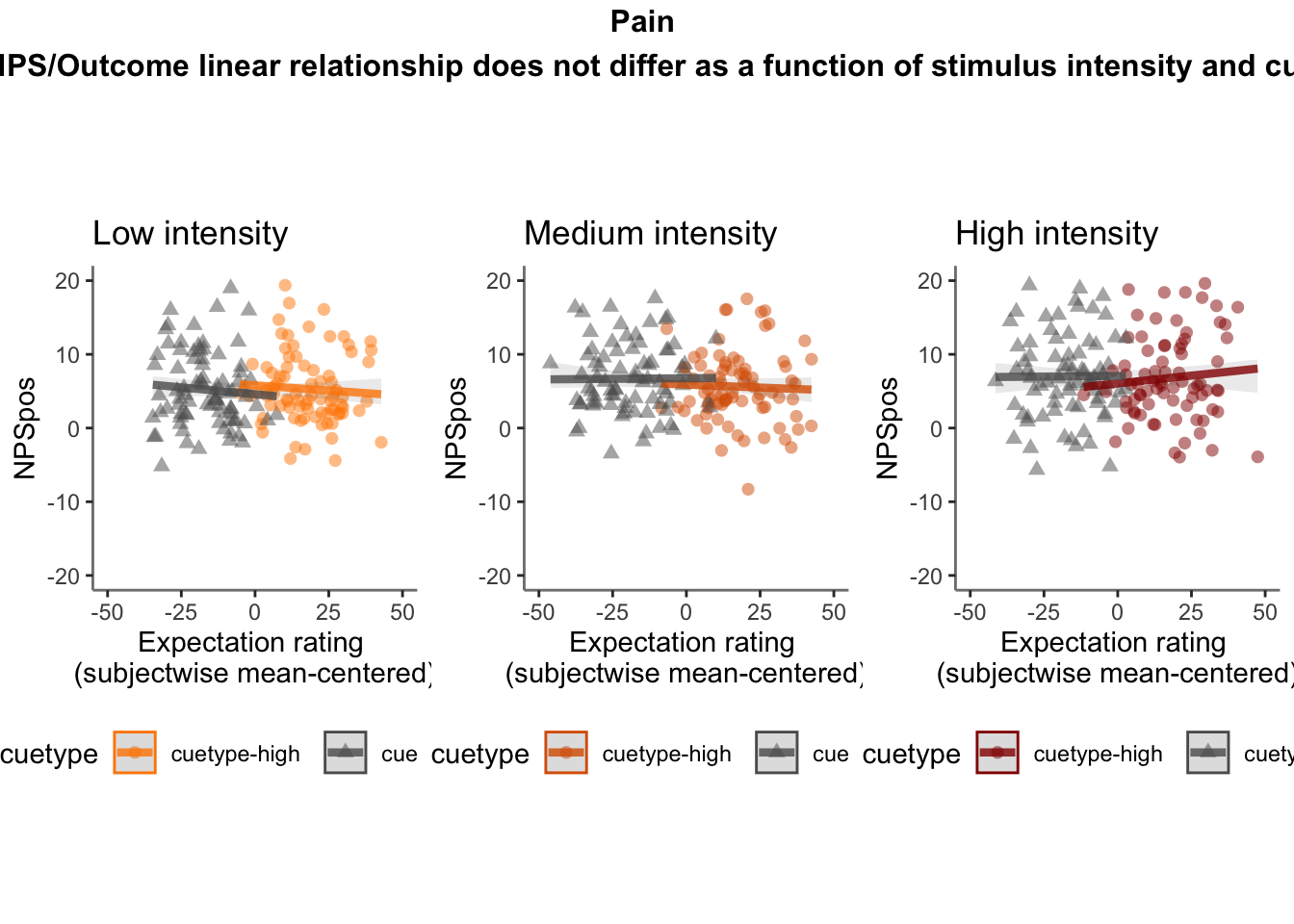
cue_high = demean_dropna[demean_dropna$cue_name == "high", ]
fig.height = 50
fig.width = 10
ggplot(aes(x=EXPECT_demean, y=NPSpos), data=cue_high) +
  geom_smooth(method='lm', se=F, size=0.75) +
  geom_point(size=0.1) + 
    # geom_abline(intercept = 0, slope = 1, color="green", 
    #              linetype="dashed", size=0.5) +
  facet_wrap(~sub) + 
  theme(legend.position='none') + 
  xlim(-50,50) + ylim(-50,50) +
  xlab("raw data from each participant: n-1 lagged outcome angle") + 
  ylab("n current expectation rating")

## `geom_smooth()` using formula = 'y ~ x'

## Warning: Removed 132 rows containing non-finite values (`stat_smooth()`).

## Warning: Removed 132 rows containing missing values (`geom_point()`).

cue_low = demean_dropna[demean_dropna$cue_name == "low", ]
fig.height = 50
fig.width = 10
ggplot(aes(x=EXPECT_demean, y=NPSpos), data=cue_low) +
  geom_smooth(method='lm', se=F, size=0.75) +
  geom_point(size=0.1) + 
    # geom_abline(intercept = 0, slope = 1, color="green", 
    #              linetype="dashed", size=0.5) +
  facet_wrap(~sub) + 
  theme(legend.position='none') + 
  xlim(-50,50) + ylim(-50,50) +
  xlab("raw data from each participant: n-1 lagged outcome angle") + 
  ylab("n current expectation rating")

## `geom_smooth()` using formula = 'y ~ x'

## Warning: Removed 137 rows containing non-finite values (`stat_smooth()`).

## Warning: Removed 137 rows containing missing values (`geom_point()`).

26.5.4.1 facetwrap

# 74, 85, 118
fig.height = 50
fig.width = 10
ggplot(aes(x=EXPECT_demean, y=NPSpos), data=demean_high) +
  geom_smooth(method='lm', se=F, size=0.75) +
  geom_point(size=0.1) + 
    # geom_abline(intercept = 0, slope = 1, color="green", 
    #              linetype="dashed", size=0.5) +
  facet_wrap(~sub) + 
  theme(legend.position='none') + 
  xlim(-50,50) + ylim(-50,50) +
  xlab("raw data from each participant: n-1 lagged outcome angle") + 
  ylab("n current expectation rating")

## `geom_smooth()` using formula = 'y ~ x'

## Warning: Removed 87 rows containing non-finite values (`stat_smooth()`).

## Warning: Removed 87 rows containing missing values (`geom_point()`).

# 74, 85, 118, 117
fig.height = 50
fig.width = 10
ggplot(aes(x=EXPECT_demean, y=NPSpos), data=demean_low) +
  geom_smooth(method='lm', se=F, size=0.75) +
  geom_point(size=0.1) + 
    # geom_abline(intercept = 0, slope = 1, color="green", 
    #              linetype="dashed", size=0.5) +
  facet_wrap(~sub) + 
  theme(legend.position='none') + 
  xlim(-50,50) + ylim(-50,50) +
  xlab("raw data from each participant: n-1 lagged outcome angle") + 
  ylab("n current expectation rating")

## `geom_smooth()` using formula = 'y ~ x'

## Warning: Removed 92 rows containing non-finite values (`stat_smooth()`).

## Warning: Removed 92 rows containing missing values (`geom_point()`).

# 74, 85, 118, 117
fig.height = 50
fig.width = 10
ggplot(aes(x=EXPECT_demean, y=NPSpos), data=demean_med) +
  geom_smooth(method='lm', se=F, size=0.75) +
  geom_point(size=0.1) + 
    # geom_abline(intercept = 0, slope = 1, color="green", 
    #              linetype="dashed", size=0.5) +
  facet_wrap(~sub) + 
  theme(legend.position='none') + 
  xlim(-50,50) + ylim(-50,50) +
  xlab("raw data from each participant: n-1 lagged outcome angle") + 
  ylab("n current expectation rating")

## `geom_smooth()` using formula = 'y ~ x'

## Warning: Removed 90 rows containing non-finite values (`stat_smooth()`).

## Warning: Removed 90 rows containing missing values (`geom_point()`).

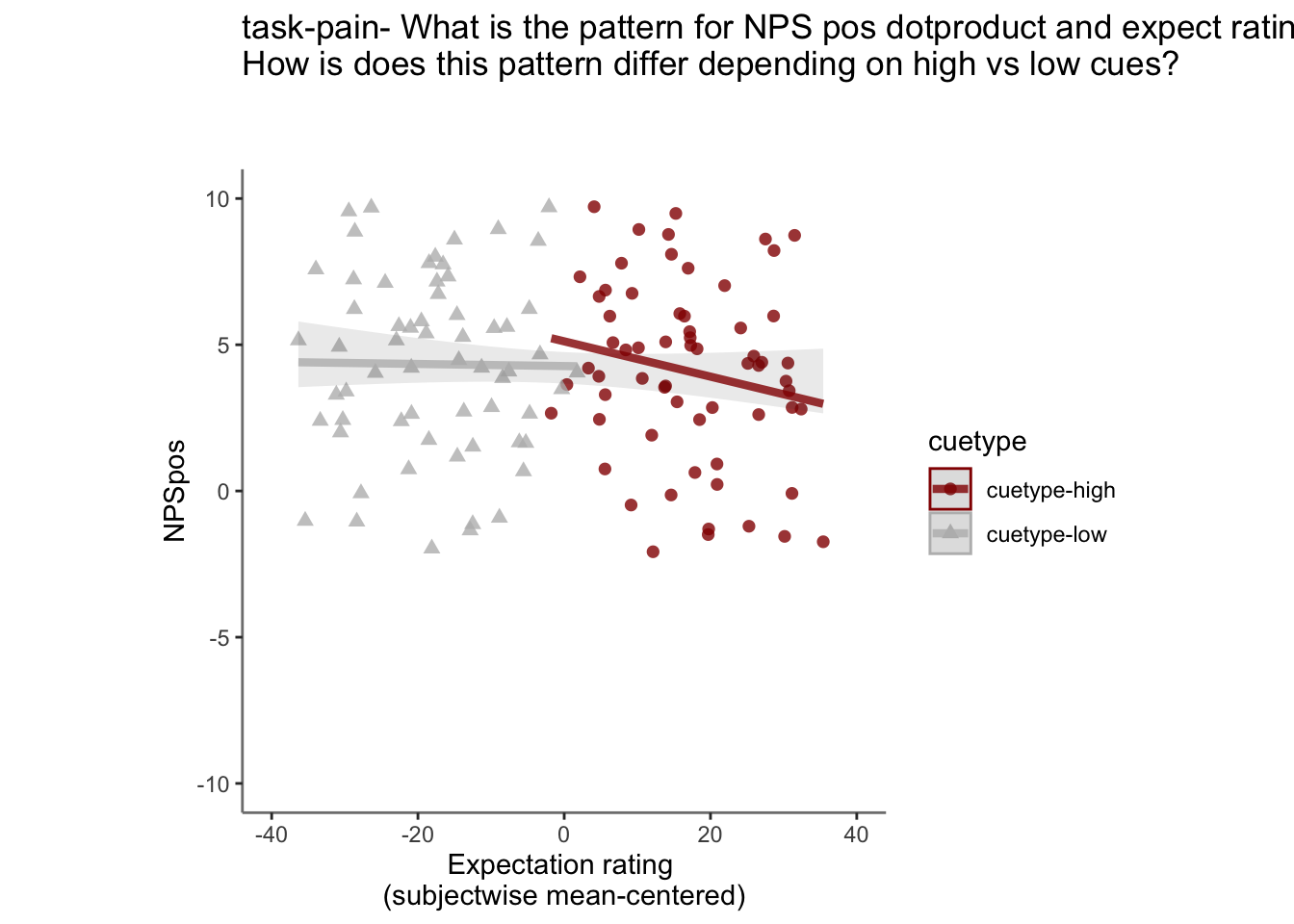
#### subjectwise plot v2

ggplot(demean_med, aes(y = NPSpos, 
                       x = EXPECT_demean, 
                       colour = cuetype, shape = sub), size = .3, color = 'gray') + 
  geom_point(size = .1) + 
  geom_smooth(method = 'lm', formula= y ~ x, se = FALSE, size = .3) +
  scale_color_manual(values = c("cuetype-high" = "#941100", "cuetype-low" = "#BBBBBB"), ) +
  theme_classic()

## Warning: The shape palette can deal with a maximum of 6 discrete values because
## more than 6 becomes difficult to discriminate; you have 85. Consider
## specifying shapes manually if you must have them.

## Warning: Removed 1170 rows containing missing values (`geom_point()`).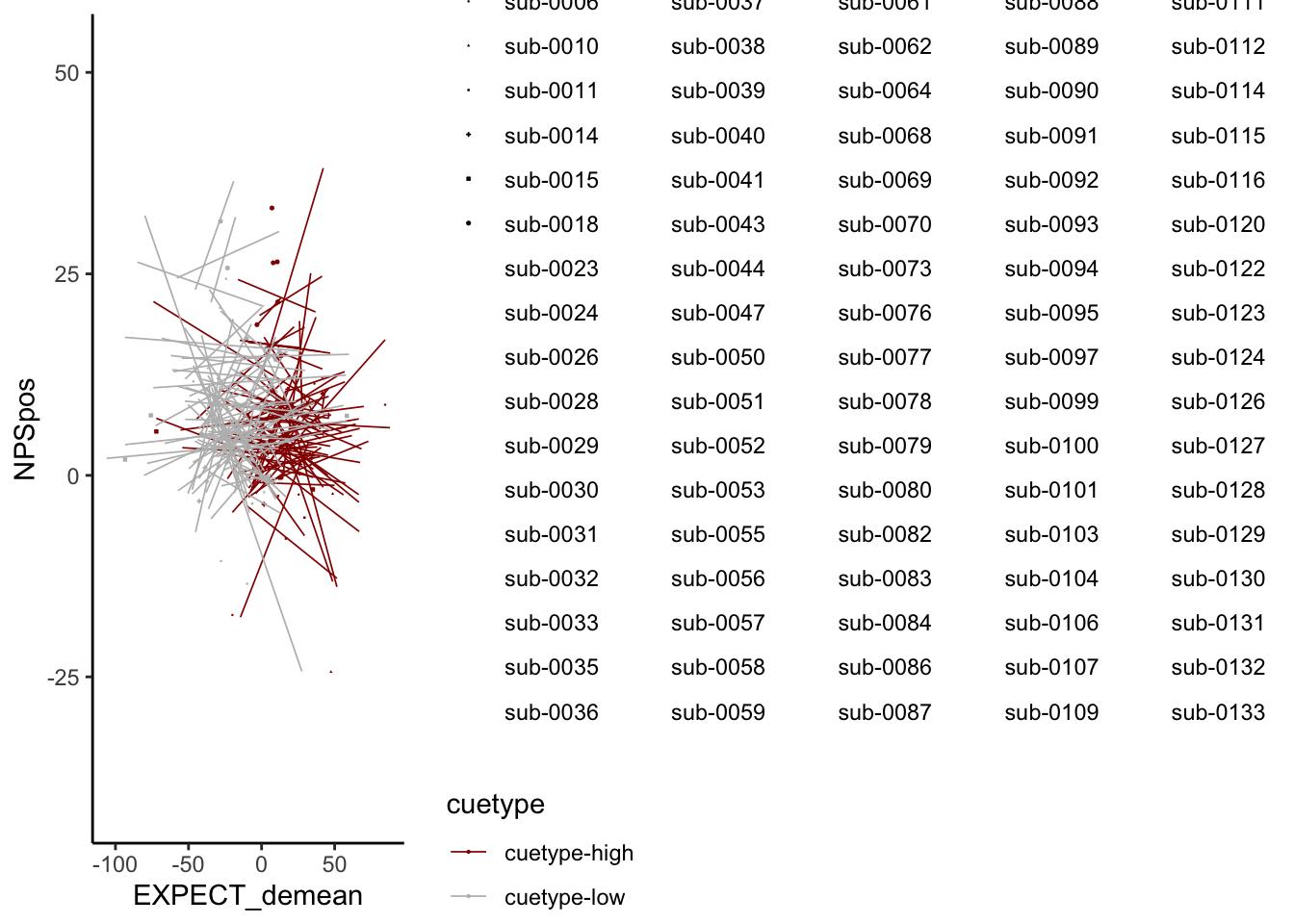

26.5.4.2 subjetwise plot

26.5.5 ACCURATE Is this statistically significant?

26.5.5.1 ACCURATE: NPS ~ demean + CMC

model.npsexpectdemean <- lmer(NPSpos ~ 
                          CUE_high_gt_low*STIM_linear*EXPECT_demean +CUE_high_gt_low*STIM_quadratic*EXPECT_demean + factor(ses) +  EXPECT_cmc +
                          (1 |sub), data = demean_dropna
                    ) 
# CUE_high_gt_low+STIM+EXPECT_demean
sjPlot::tab_model(model.npsexpectdemean,
                  title = "Multilevel-modeling: \nlmer(NPSpos ~ CUE * STIM * EXPECT_demean + (1| sub), data = pvc)",
                  CSS = list(css.table = '+font-size: 12;'))

Multilevel-modeling: lmer(NPSpos ~ CUE * STIM * EXPECT_demean + (1| sub), data = pvc)
	NPSpos
Predictors	Estimates	CI	p
(Intercept)	6.65	5.42 – 7.88	<0.001
CUE high gt low	-0.70	-1.35 – -0.05	0.034
STIM linear	2.25	1.46 – 3.04	<0.001
EXPECT demean	-0.00	-0.01 – 0.01	0.752
STIM quadratic	-0.22	-0.92 – 0.47	0.529
factor(ses)ses-03	0.09	-0.61 – 0.78	0.808
factor(ses)ses-04	1.10	0.42 – 1.79	0.002
EXPECT cmc	0.07	0.03 – 0.12	0.002
CUE high gt low * STIM linear	-1.12	-2.70 – 0.46	0.166
CUE high gt low * EXPECT demean	-0.02	-0.04 – 0.01	0.199
STIM linear * EXPECT demean	0.01	-0.02 – 0.04	0.500
CUE high gt low * STIM quadratic	-0.40	-1.80 – 0.99	0.571
EXPECT demean * STIM quadratic	-0.02	-0.04 – 0.01	0.180
(CUE high gt low * STIM linear) * EXPECT demean	0.03	-0.03 – 0.08	0.339
(CUE high gt low * EXPECT demean) * STIM quadratic	0.04	-0.01 – 0.08	0.160
Random Effects
σ²	63.19
τ₀₀ _sub	26.99
ICC	0.30
N _sub	86
Observations	3765
Marginal R² / Conditional R²	0.050 / 0.335

26.5.5.2 simple slopes when STIM == ‘high’, EXPECT_demean slope difference between high vs. low cue

interactions::sim_slopes(model=model.npsexpectdemean, pred=EXPECT_demean, modx=CUE_high_gt_low, mod2 =STIM_linear, mod2.values = 0.5, centered = 'all', data = demean_dropna)

## Using data demean_dropna from global environment. This could cause
## incorrect results if demean_dropna has been altered since the model was
## fit. You can manually provide the data to the "data =" argument.

## ███████████████████ While STIM_linear (2nd moderator) = 0.50 ███████████████████ 
## 
## JOHNSON-NEYMAN INTERVAL 
## 
## The Johnson-Neyman interval could not be found. Is the p value for your
## interaction term below the specified alpha?
## 
## SIMPLE SLOPES ANALYSIS 
## 
## Slope of EXPECT_demean when CUE_high_gt_low = -0.50 (-0.5): 
## 
##   Est.   S.E.   t val.      p
## ------ ------ -------- ------
##   0.00   0.01     0.36   0.72
## 
## Slope of EXPECT_demean when CUE_high_gt_low =  0.50 (0.5): 
## 
##   Est.   S.E.   t val.      p
## ------ ------ -------- ------
##   0.00   0.01     0.11   0.91

26.5.5.3 emtrneds

emt.t <- emtrends(model.npsexpectdemean, ~ STIM_linear | CUE_high_gt_low, 
         var = "EXPECT_demean", 
         # nuisance = c("EXPECT_cmc"),
         at = list(STIM_linear=c(0.5, 0, -0.5)),
         lmer.df = "asymp")
pairs(emt.t, simple = "each")

## $`simple contrasts for STIM_linear`
## CUE_high_gt_low = -0.5:
##  contrast                           estimate      SE  df z.ratio p.value
##  STIM_linear0.5 - STIM_linear0      -0.00201 0.00962 Inf  -0.208  0.9763
##  STIM_linear0.5 - (STIM_linear-0.5) -0.00401 0.01925 Inf  -0.208  0.9763
##  STIM_linear0 - (STIM_linear-0.5)   -0.00201 0.00962 Inf  -0.208  0.9763
## 
## CUE_high_gt_low =  0.5:
##  contrast                           estimate      SE  df z.ratio p.value
##  STIM_linear0.5 - STIM_linear0       0.01164 0.01053 Inf   1.105  0.5111
##  STIM_linear0.5 - (STIM_linear-0.5)  0.02327 0.02106 Inf   1.105  0.5111
##  STIM_linear0 - (STIM_linear-0.5)    0.01164 0.01053 Inf   1.105  0.5111
## 
## Results are averaged over the levels of: STIM_quadratic, ses 
## Degrees-of-freedom method: asymptotic 
## P value adjustment: tukey method for comparing a family of 3 estimates 
## 
## $`simple contrasts for CUE_high_gt_low`
## STIM_linear = -0.5:
##  contrast                                   estimate     SE  df z.ratio p.value
##  (CUE_high_gt_low-0.5) - CUE_high_gt_low0.5  0.02426 0.0194 Inf   1.249  0.2117
## 
## STIM_linear =  0.0:
##  contrast                                   estimate     SE  df z.ratio p.value
##  (CUE_high_gt_low-0.5) - CUE_high_gt_low0.5  0.01061 0.0134 Inf   0.793  0.4276
## 
## STIM_linear =  0.5:
##  contrast                                   estimate     SE  df z.ratio p.value
##  (CUE_high_gt_low-0.5) - CUE_high_gt_low0.5 -0.00303 0.0197 Inf  -0.154  0.8779
## 
## Results are averaged over the levels of: STIM_quadratic, ses 
## Degrees-of-freedom method: asymptotic

# contrast(emt.t, "revpairwise")