Chapter 28 [fMRI] NPS ~ singletrial

What is the purpose of this notebook?

  • Here, I model NPS dot products as a function of cue, stimulus intensity and expectation ratings.
  • One of the findings is that low cues lead to higher NPS dotproducts in the high intensity group, and that this effect becomes non-significant across sessions.
  • 03/23/2023: For now, I’m grabbing participants that have complete data, i.e. 18 runs, all three sessions.

28.1 NPS ~ 3 task * 3 stimulus_intensity

Q. What does the NPS pattern look like for the three tasks?

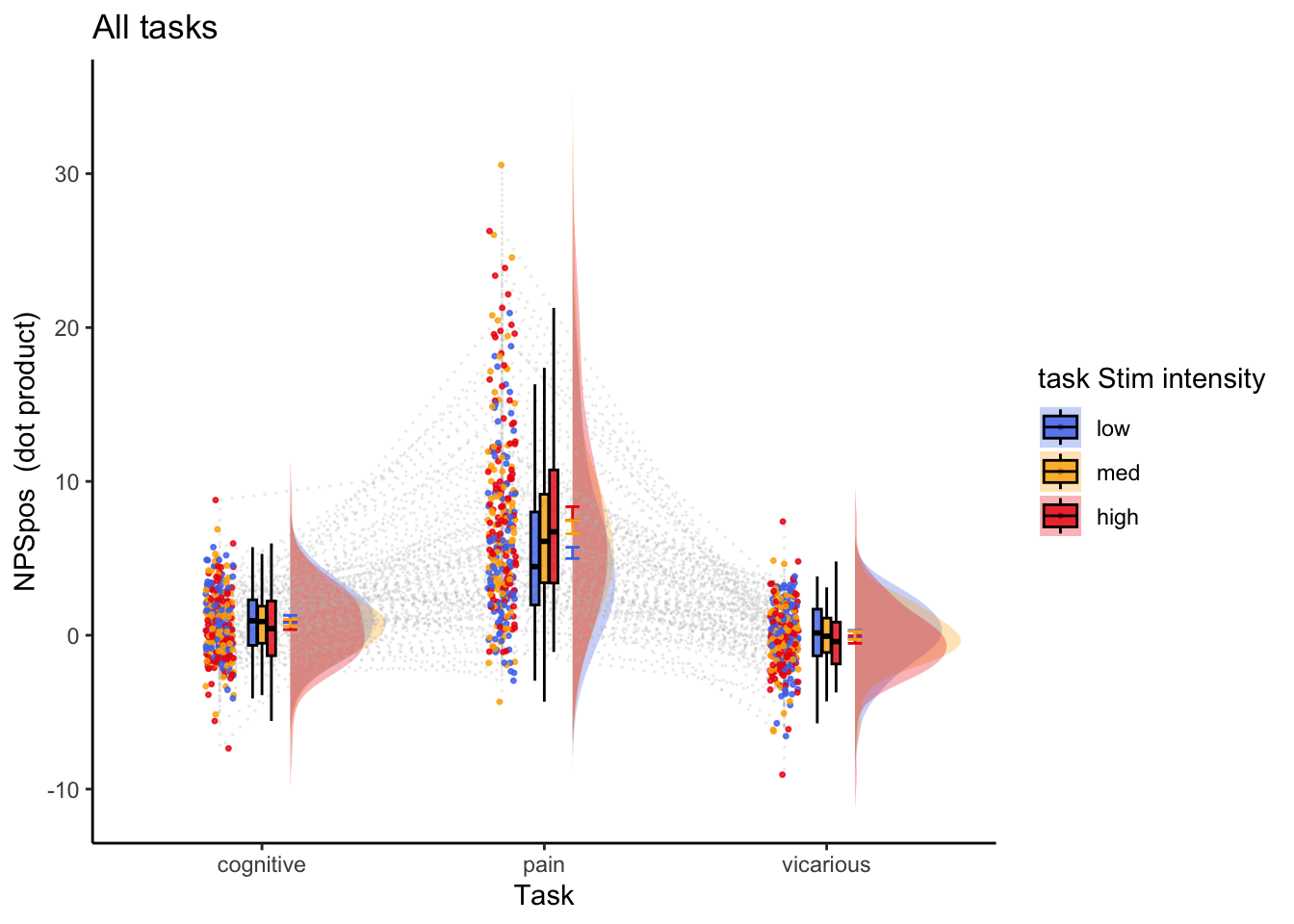
Contrast weight table

Table 28.1: Contrast weights
pain vicarious cognitive
task_V_gt_C 0.00 0.50 -0.50
task_P_gt_VC 0.66 -0.34 -0.34
Multilevel-modeling: lmer(NPSpos ~ task_V_gt_CSTIM + task_P_gt_VCSTIM + (task|sub), data = pvc)
  NPSpos
Predictors Estimates CI p
(Intercept) 2.80 2.38 – 3.22 <0.001
task V gt C -0.86 -1.36 – -0.36 0.001
STIM [low] -0.56 -0.82 – -0.31 <0.001
STIM [med] -0.18 -0.43 – 0.07 0.168
task P gt VC 7.86 6.75 – 8.96 <0.001
task V gt C * STIM [low] 0.03 -0.58 – 0.64 0.918
task V gt C * STIM [med] 0.03 -0.58 – 0.64 0.926
STIM [low] * task P gt VC -2.75 -3.29 – -2.20 <0.001
STIM [med] * task P gt VC -1.17 -1.71 – -0.62 <0.001
Random Effects
σ2 53.62
τ00 sub 2.40
τ11 sub.taskpain 30.06
τ11 sub.taskvicarious 1.69
ρ01 -0.21
-0.62
ICC 0.04
N sub 111
Observations 19428
Marginal R2 / Conditional R2 0.147 / 0.183

Eta squared

Parameter Eta2_partial CI CI_low CI_high
task_V_gt_C 0.1751578 0.95 0.0774378 1
STIM 0.0010482 0.95 0.0003778 1
task_P_gt_VC 0.5790305 0.95 0.4818733 1
task_V_gt_C:STIM 0.0000007 0.95 0.0000000 1
STIM:task_P_gt_VC 0.0051178 0.95 0.0035162 1

Cohen’s d

t df d
task_V_gt_C -3.3999806 409.2144 -0.3361483
STIMlow -4.3779053 19097.0393 -0.0633597
STIMmed -1.3797123 19097.0393 -0.0199680
task_P_gt_VC 13.9522425 126.9874 2.4762455
task_V_gt_C:STIMlow 0.1034714 19097.0393 0.0014975
task_V_gt_C:STIMmed 0.0933040 19097.0393 0.0013504
STIMlow:task_P_gt_VC -9.8736649 19097.0393 -0.1428977
STIMmed:task_P_gt_VC -4.1879665 19097.0393 -0.0606108

28.2 NPS ~ paintask: 2 cue x 3 stimulus_intensity

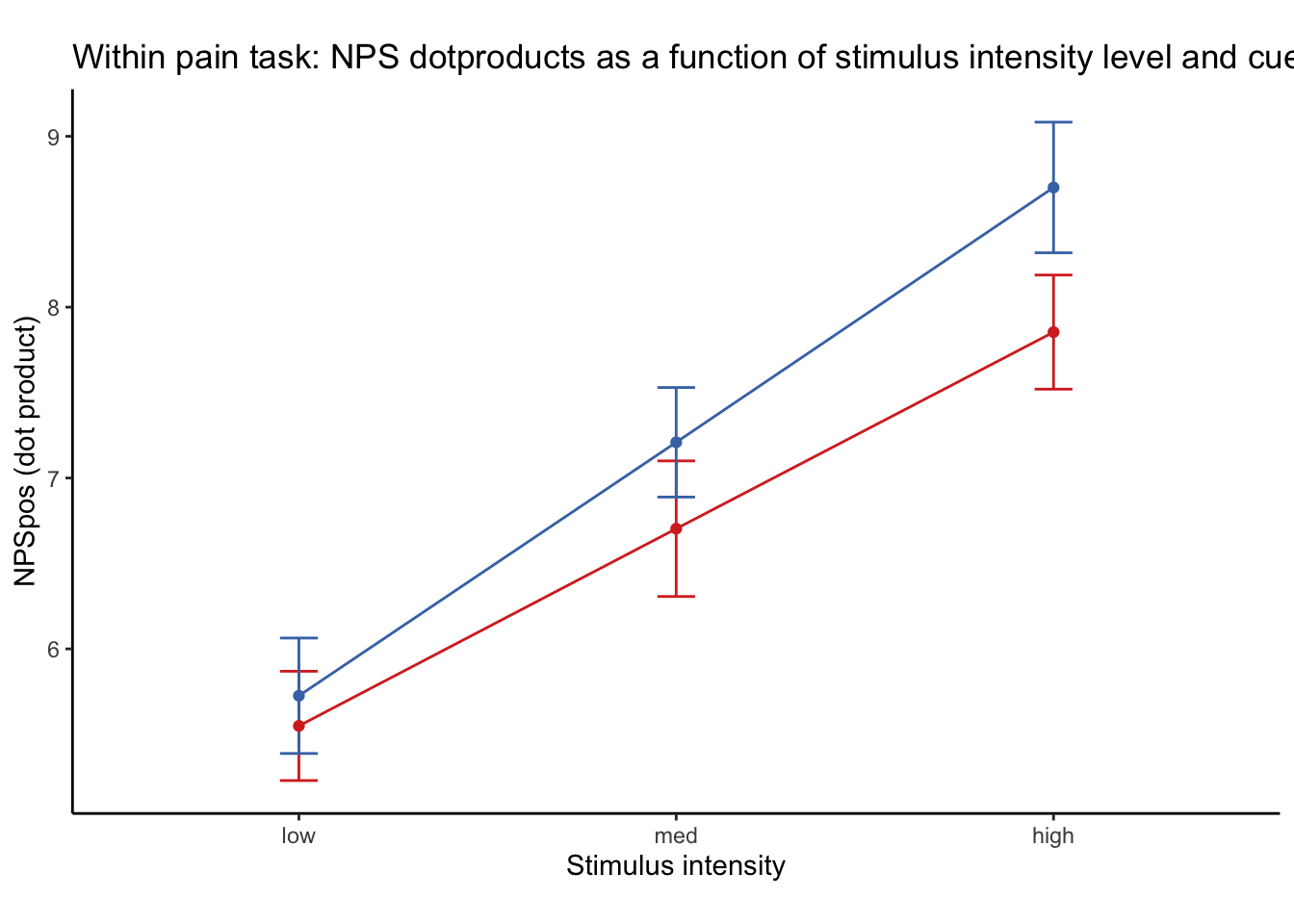
Q. Within pain task, Does stimulus intenisty level and cue level significantly predict NPS dotproducts?

Lineplots

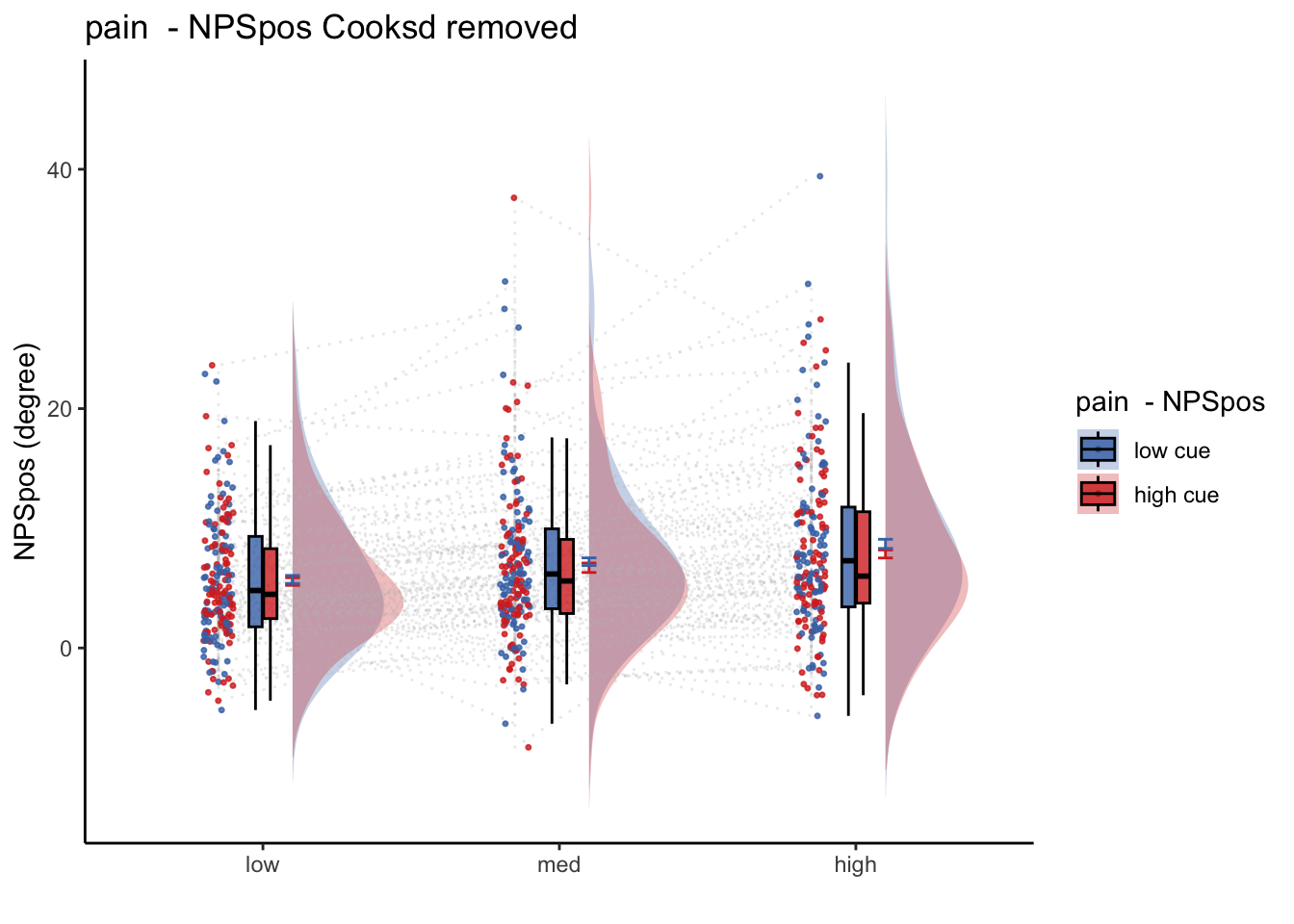
28.2.1 Linear model results (NPS ~ paintask: 2 cue x 3 stimulus_intensity)

model.npscuestim <- lmer(NPSpos ~ 
                          CUE_high_gt_low*STIM_linear +CUE_high_gt_low * STIM_quadratic +
                          (CUE_high_gt_low+STIM|sub), data = data_screen
                    )
sjPlot::tab_model(model.npscuestim,
                  title = "Multilevel-modeling: \nlmer(NPSpos ~ CUE * STIM + (CUE + STIM | sub), data = pvc)",
                  CSS = list(css.table = '+font-size: 12;'))
Multilevel-modeling: lmer(NPSpos ~ CUE * STIM + (CUE + STIM | sub), data = pvc)
  NPSpos
Predictors Estimates CI p
(Intercept) 6.91 5.79 – 8.02 <0.001
CUE high gt low -0.68 -1.21 – -0.15 0.012
STIM linear 2.61 1.94 – 3.28 <0.001
STIM quadratic -0.06 -0.59 – 0.47 0.831
CUE high gt low * STIM
linear 		-0.66 -1.83 – 0.52 0.276
CUE high gt low * STIM
quadratic 		-0.51 -1.55 – 0.52 0.332
Random Effects
σ2 62.27
τ00 sub 38.74
τ11 sub.CUE_high_gt_low 1.08
τ11 sub.STIMlow 2.41
τ11 sub.STIMmed 1.56
ρ01 -0.58
-0.97
-0.87
ICC 0.39
N sub 96
Observations 4133
Marginal R2 / Conditional R2 0.013 / 0.393

Linear model eta-squared

Parameter Eta2_partial CI CI_low CI_high
CUE_high_gt_low 0.0544283 0.95 0.0061692 1
STIM_linear 0.2573057 0.95 0.1686383 1
STIM_quadratic 0.0001205 0.95 0.0000000 1
CUE_high_gt_low:STIM_linear 0.0002992 0.95 0.0000000 1
CUE_high_gt_low:STIM_quadratic 0.0002370 0.95 0.0000000 1

Linear model Cohen’s d: NPS stimulus_intensity d = 1.16, cue d = 0.45

t df d
CUE_high_gt_low -2.5003847 108.6134 -0.4798386
STIM_linear 7.6306084 168.0657 1.1771984
STIM_quadratic -0.2128945 376.0848 -0.0219559
CUE_high_gt_low:STIM_linear -1.0903230 3971.4439 -0.0346028
CUE_high_gt_low:STIM_quadratic -0.9699227 3968.1934 -0.0307943

28.2.2 2 cue * 3 stimulus_intensity * expectation_rating

data_screen$EXPECT <- data_screen$event02_expect_angle
model.nps3factor <- lmer(NPSpos ~ 
                          CUE_high_gt_low*STIM_linear*EXPECT +
                           CUE_high_gt_low*STIM_quadratic*EXPECT +
                          (CUE_high_gt_low+STIM + EXPECT|sub), data = data_screen
                    )
## boundary (singular) fit: see help('isSingular')
sjPlot::tab_model(model.nps3factor,
                  title = "Multilevel-modeling: \nlmer(NPSpos ~ CUE * STIM * EXPECTATION + (CUE + STIM + EXPECT | sub), data = pvc)",
                  CSS = list(css.table = '+font-size: 12;'))
Multilevel-modeling: lmer(NPSpos ~ CUE * STIM * EXPECTATION + (CUE + STIM + EXPECT | sub), data = pvc)
  NPSpos
Predictors Estimates CI p
(Intercept) 6.51 5.46 – 7.56 <0.001
CUE high gt low -0.61 -1.81 – 0.59 0.320
STIM linear 1.66 0.36 – 2.96 0.013
EXPECT 0.00 -0.01 – 0.02 0.642
STIM quadratic 0.57 -0.54 – 1.67 0.314
CUE high gt low * STIM
linear 		-2.16 -4.63 – 0.31 0.086
CUE high gt low * EXPECT -0.00 -0.02 – 0.01 0.793
STIM linear * EXPECT 0.01 -0.00 – 0.03 0.153
CUE high gt low * STIM
quadratic 		-1.38 -3.55 – 0.78 0.211
EXPECT * STIM quadratic -0.01 -0.03 – 0.00 0.125
(CUE high gt low * STIM
linear) * EXPECT 		0.01 -0.02 – 0.05 0.400
(CUE high gt low
EXPECT) STIM quadratic 		0.02 -0.01 – 0.05 0.204
Random Effects
σ2 61.68
τ00 sub 18.78
τ11 sub.CUE_high_gt_low 4.00
τ11 sub.STIMlow 2.68
τ11 sub.STIMmed 1.69
τ11 sub.EXPECT 0.00
ρ01 -0.82
-0.82
-0.54
0.78
N sub 96
Observations 3991
Marginal R2 / Conditional R2 0.022 / NA

eta squared

Parameter Eta2_partial CI CI_low CI_high
CUE_high_gt_low 0.0048614 0.95 0.0000000 1
STIM_linear 0.0163037 0.95 0.0018659 1
EXPECT 0.0038038 0.95 0.0000000 1
STIM_quadratic 0.0016055 0.95 0.0000000 1
CUE_high_gt_low:STIM_linear 0.0008638 0.95 0.0000000 1
CUE_high_gt_low:EXPECT 0.0002676 0.95 0.0000000 1
STIM_linear:EXPECT 0.0037328 0.95 0.0000000 1
CUE_high_gt_low:STIM_quadratic 0.0004397 0.95 0.0000000 1
EXPECT:STIM_quadratic 0.0030427 0.95 0.0000000 1
CUE_high_gt_low:STIM_linear:EXPECT 0.0001945 0.95 0.0000000 1
CUE_high_gt_low:EXPECT:STIM_quadratic 0.0004337 0.95 0.0000000 1

Cohen’s d

## boundary (singular) fit: see help('isSingular')
t df d
CUE_high_gt_low -0.9950365 202.6738 -0.1397881
STIM_linear 2.4959685 375.8842 0.2574791
EXPECT 0.4645983 56.5310 0.1235846
STIM_quadratic 1.0067175 630.2444 0.0802016
CUE_high_gt_low:STIM_linear -1.7178257 3413.4593 -0.0588047
CUE_high_gt_low:EXPECT -0.2626946 257.7997 -0.0327220
STIM_linear:EXPECT 1.4294626 545.3629 0.1224222
CUE_high_gt_low:STIM_quadratic -1.2514737 3560.2666 -0.0419479
EXPECT:STIM_quadratic -1.5354631 772.4962 -0.1104896
CUE_high_gt_low:STIM_linear:EXPECT 0.8410596 3636.9518 0.0278925
CUE_high_gt_low:EXPECT:STIM_quadratic 1.2712295 3724.7724 0.0416585 
## Warning: Ignoring 142 observations

28.3 NPS ~ SES * CUE * STIM

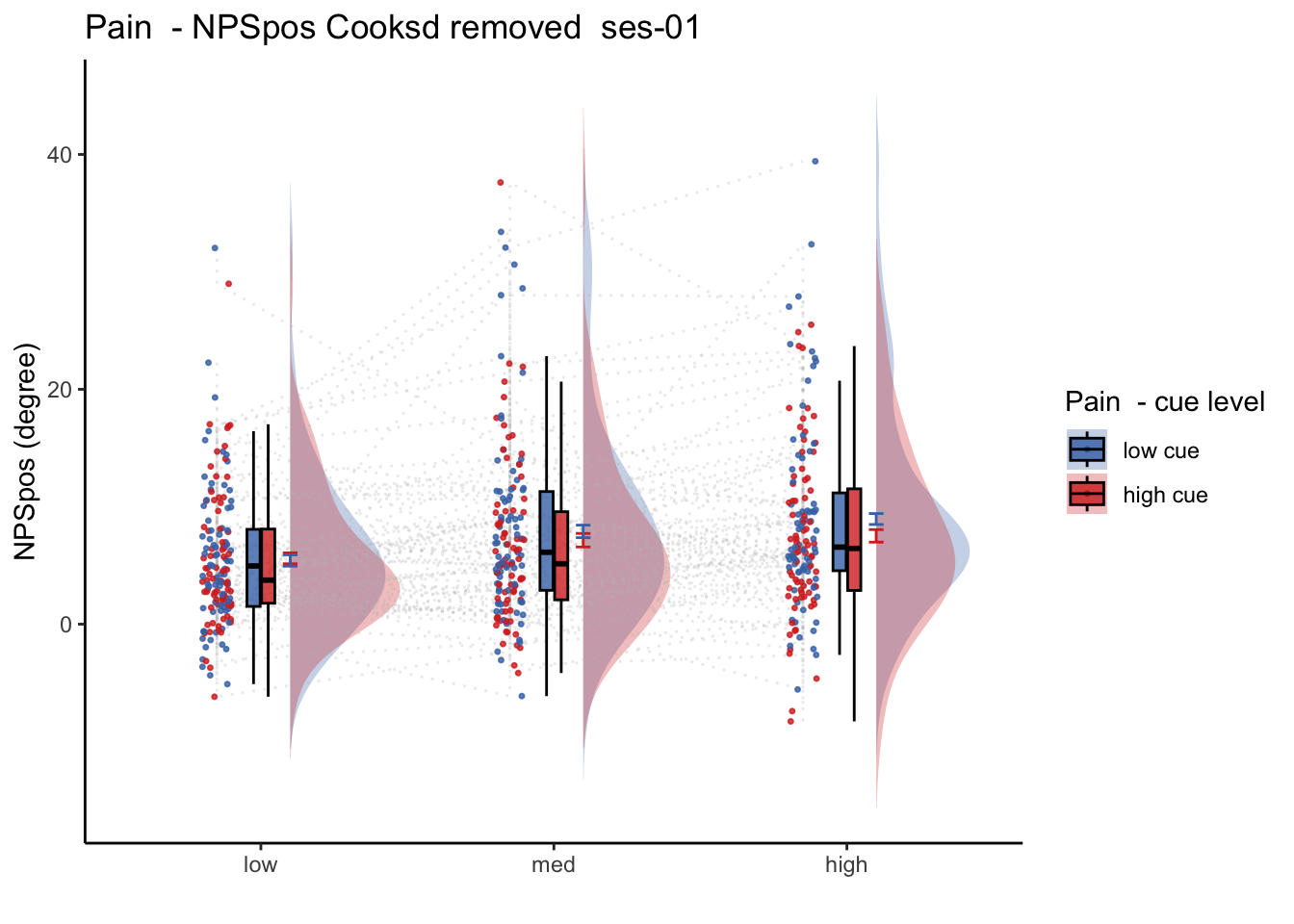
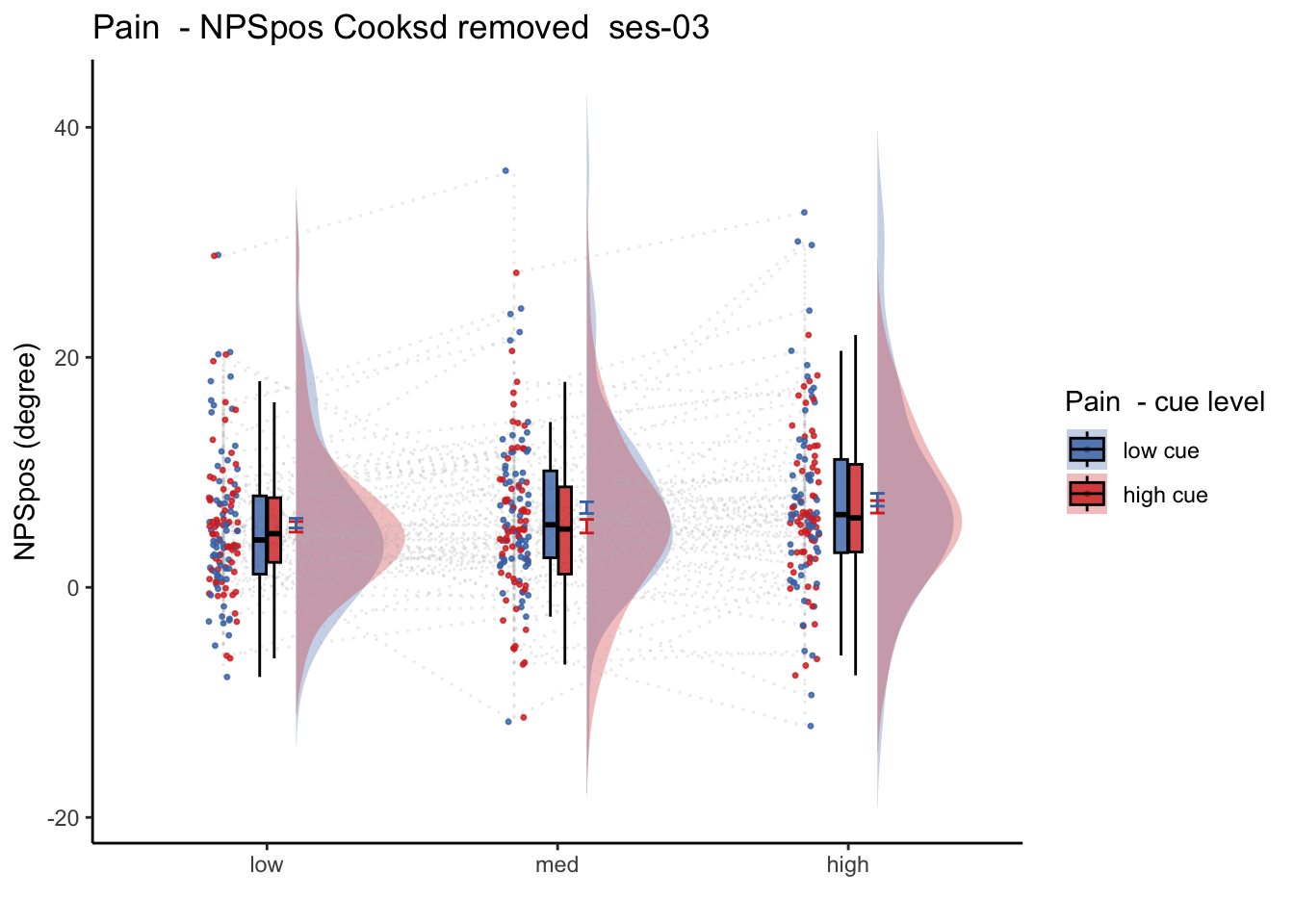
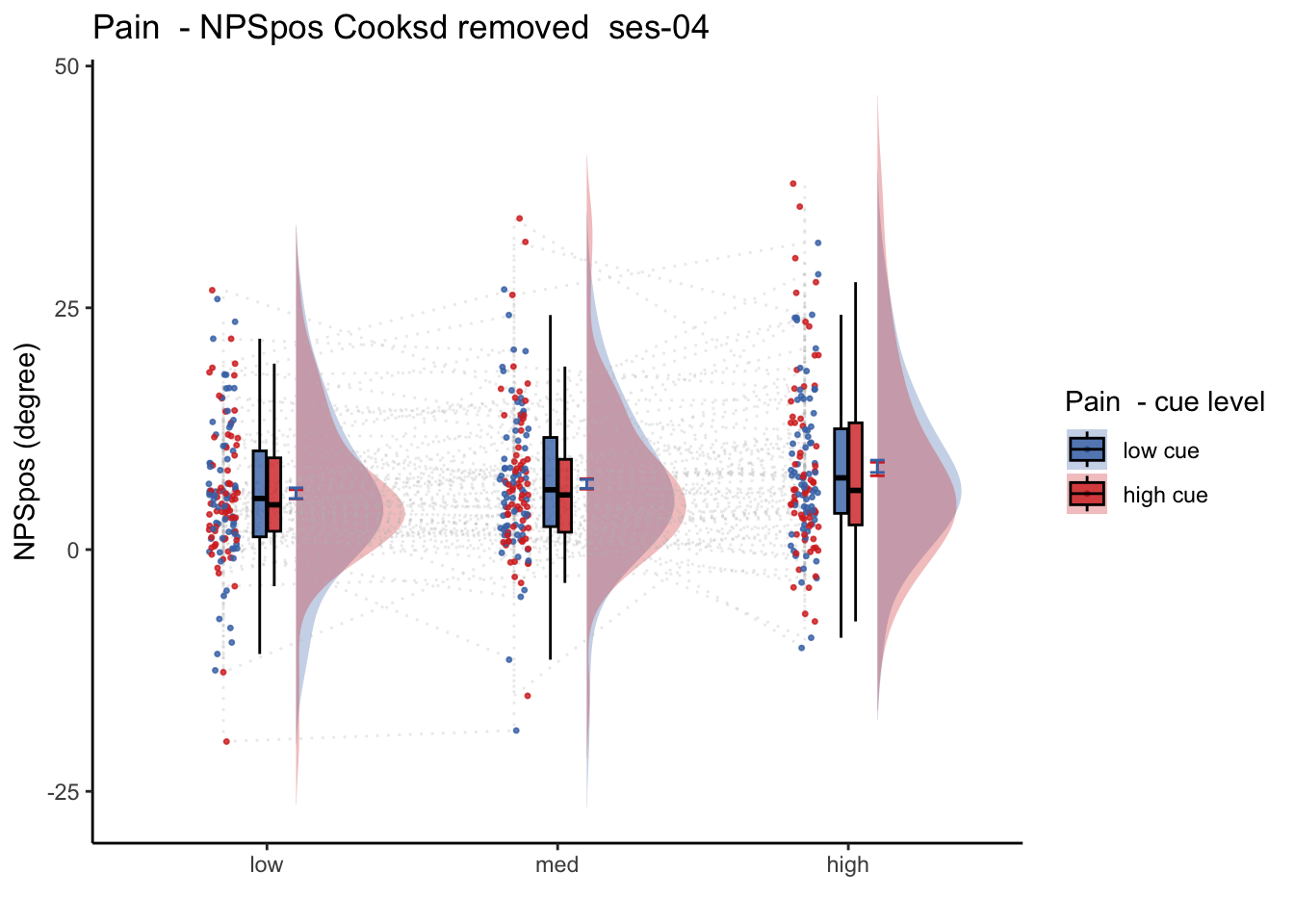
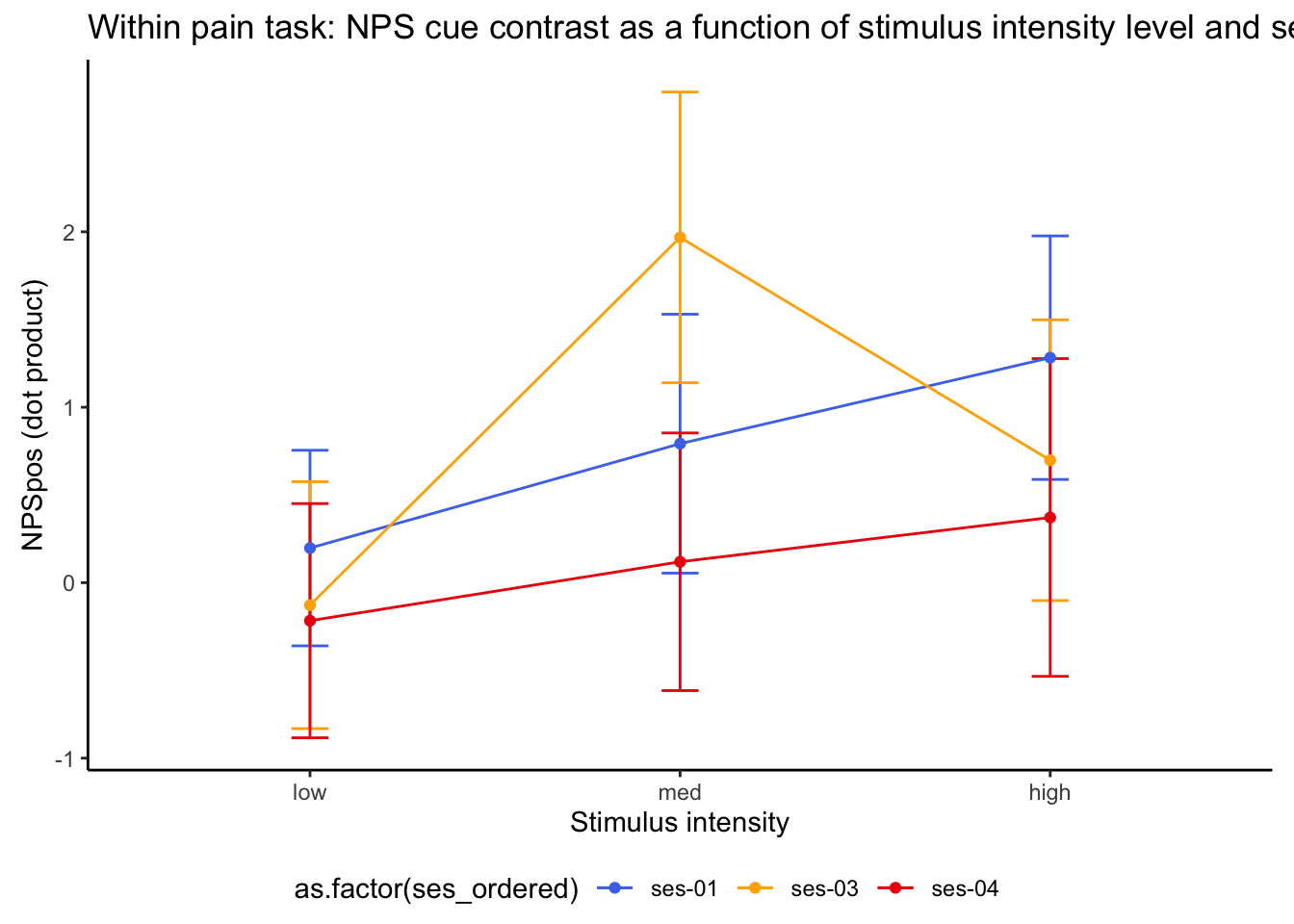
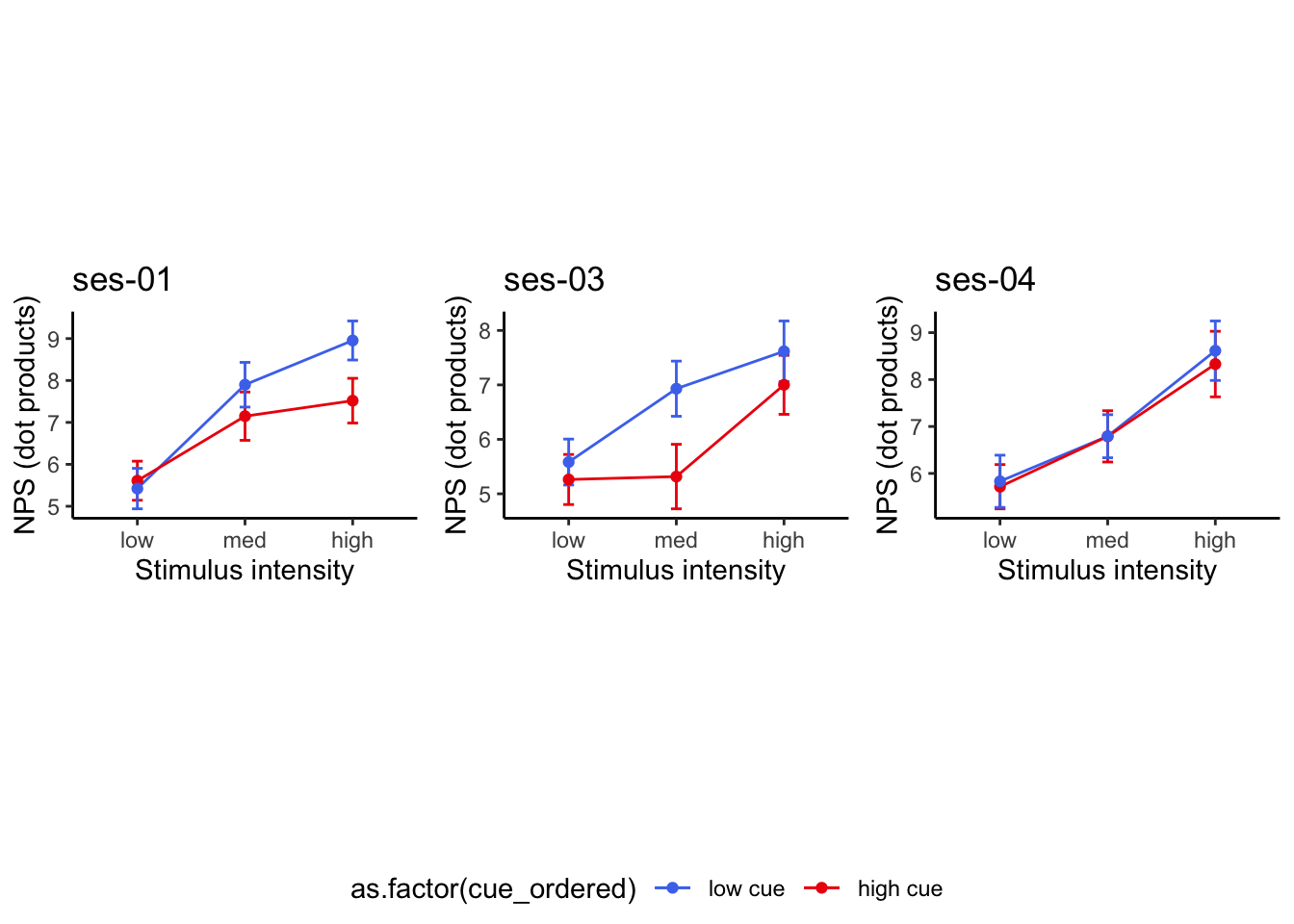
Q. Is the cue effect on NPS different across sessions?

Quick answer: Yes, the cue effect in session 1 (for high intensity group) is significantly different; whereas this different becomes non significant in session 4. To unpack, a participant was informed to experience a low stimulus intensity, when in fact they were delivered a high intensity stimulus. This violation presumably leads to a higher NPS response, given that they were delivered a much painful stimulus than expected. The fact that the cue effect is almost non significant during the last session indicates that the cue effects are not just an anchoring effect.

28.3.0.1 Session wise plots

28.3.1 Here are the stats models: NPS~session * cue * stimulus_intensity

  1. Calculate difference score
  • average high and low cue within run.
  • calculate difference between high and low cue per run
  • each participant has 6 contrast scores
  • run this as a function of stimulus intensity and sessions
## Warning: Unknown or uninitialised column: `STIM_linear`.
## Warning: Unknown or uninitialised column: `STIM_quadratic`.
## Warning: Unknown or uninitialised column: `SES_1_gt_34`.
## Warning: Unknown or uninitialised column: `SES_3_gt_4`.
## boundary (singular) fit: see help('isSingular')
## Warning: Model failed to converge with 1 negative eigenvalue: -2.0e+01
Multilevel-modeling: lmer(NPSpos ~ STIM * SESSION + (STIM + SESSION | sub), data = pvc)
  NPS_cuecontrast
Predictors Estimates CI p
(Intercept) 0.56 0.02 – 1.10 0.042
STIM linear 0.80 -0.37 – 1.97 0.179
SES 3 gt 4 0.34 -0.99 – 1.67 0.612
STIM quadratic 0.70 -0.31 – 1.70 0.174
SES 1 gt 34 0.35 -0.66 – 1.37 0.498
STIM linear * SES 3 gt 4 0.23 -2.45 – 2.91 0.868
SES 3 gt 4 * STIM
quadratic 		1.44 -0.85 – 3.73 0.217
STIM linear * SES 1 gt 34 0.80 -1.47 – 3.08 0.488
STIM quadratic * SES 1 gt
34 		-0.16 -2.13 – 1.80 0.871
Random Effects
σ2 52.68
τ00 sub 2.59
τ11 sub.SESses-03 0.07
τ11 sub.SESses-04 11.03
τ11 sub.STIMlow 4.56
τ11 sub.STIMmed 4.72
ρ01 1.00
0.20
-0.82
0.07
N sub 95
Observations 1067
Marginal R2 / Conditional R2 0.007 / NA

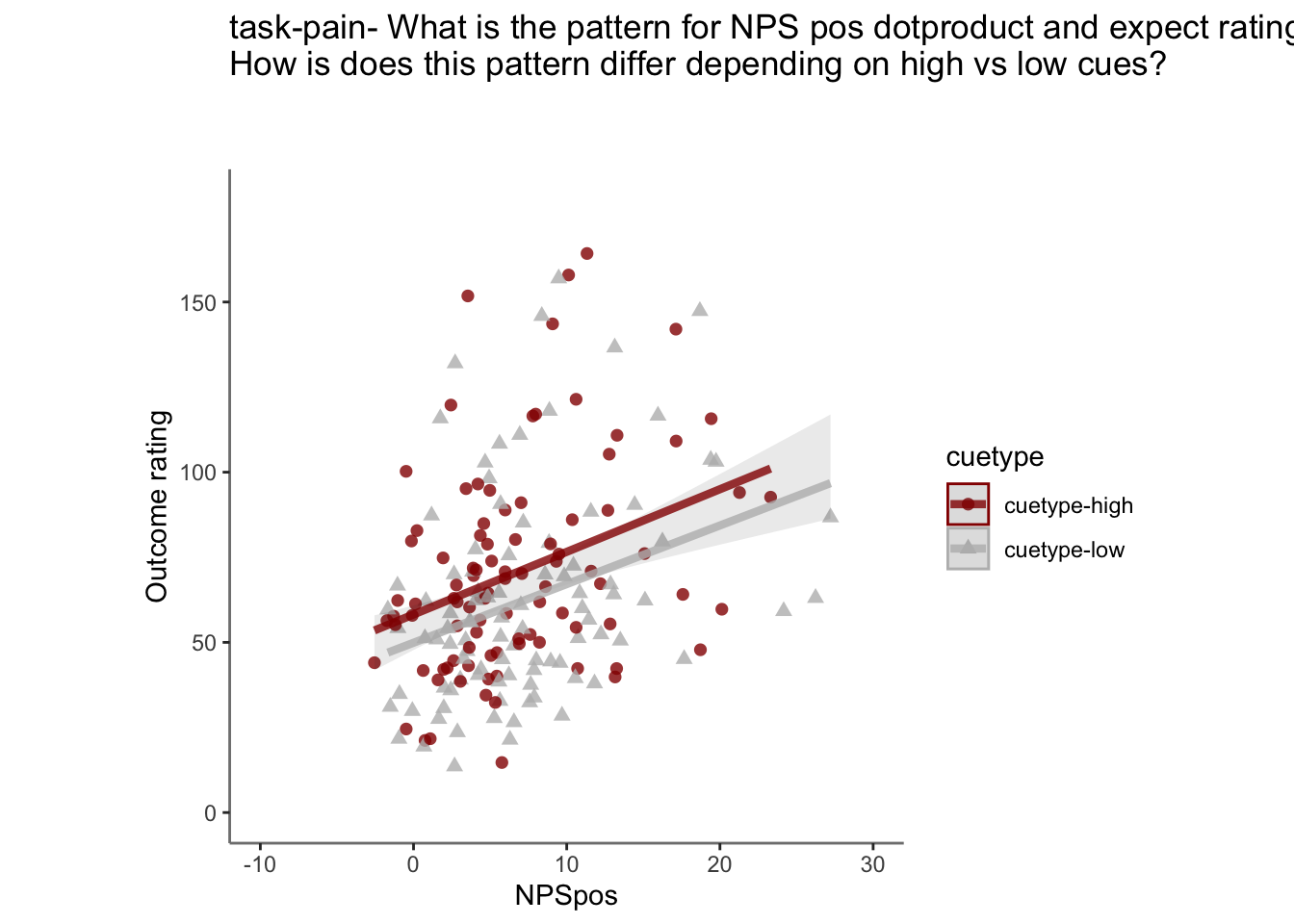
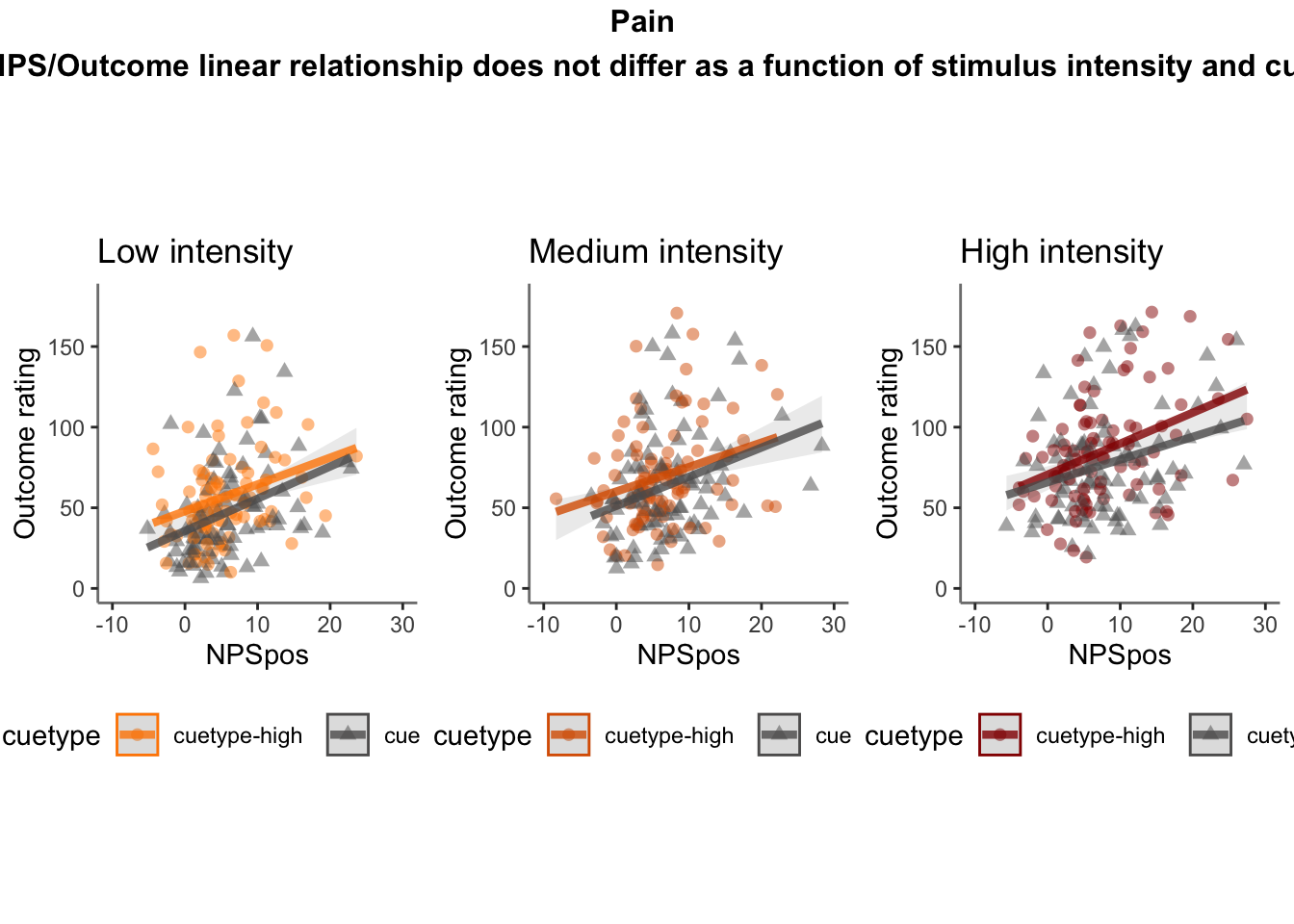
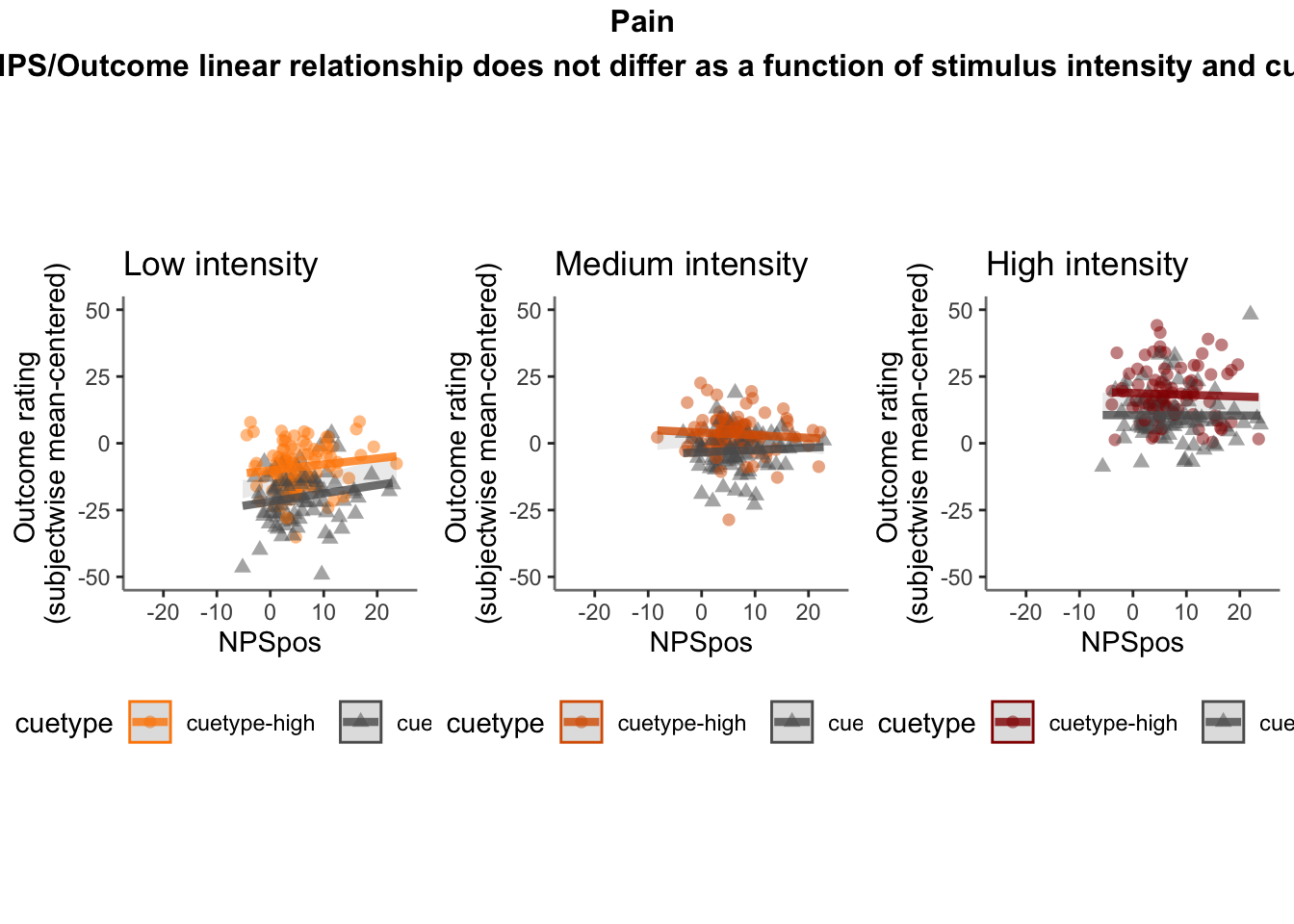
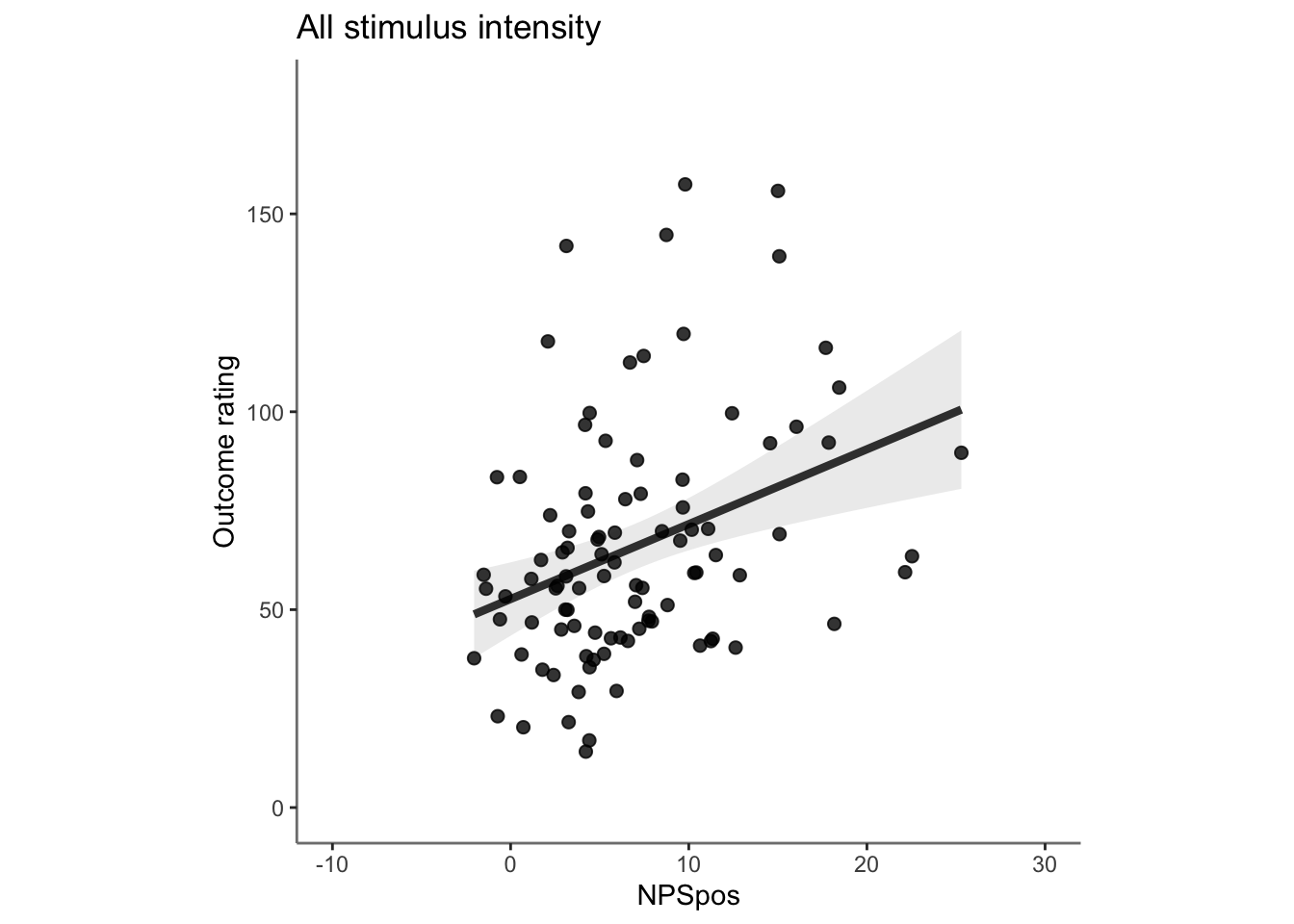
28.4 OUTCOME ~ NPS

Q. Do higher NPS values indicate higher outcome ratings? (Pain task only)

Yes, Higher NPS values are associated with higher outcome ratings. The linear relationship between NPS value and outcome ratings are stronger for conditions where cue level is congruent with stimulus intensity levels. In other words, NPS-outcome rating relationship is stringent in the low cue-low intensity group, as is the case for high cue-ghigh intensity group.

28.4.1 outcome_rating * cue

28.4.2 outcome_ratings * stimulus_intensity * cue

28.4.3 demeaned outcome rating * cue

## `geom_smooth()` using formula = 'y ~ x'
## Warning: Removed 105 rows containing non-finite values (`stat_smooth()`).
## `geom_smooth()` using formula = 'y ~ x'
## Warning: Removed 105 rows containing non-finite values (`stat_smooth()`).
## Warning: Removed 105 rows containing missing values (`geom_point()`).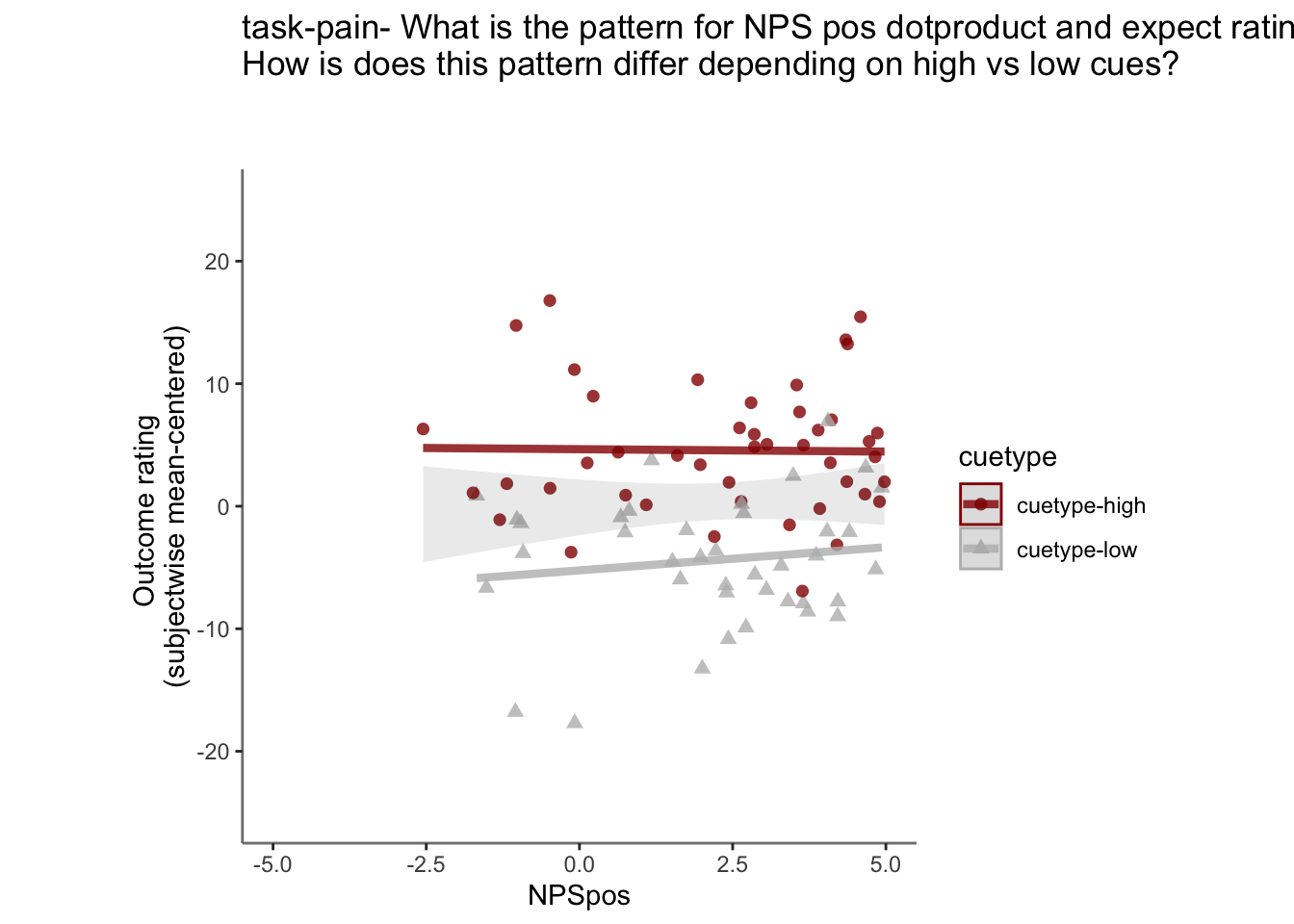

28.4.4 demeaned_outcome_ratings * stimulus_intensity * cue

28.4.5 Is this statistically significant?

# organize variable names
# NPS_demean vs. NPSpos
model.npsoutcome <- lmer(OUTCOME_demean ~ CUE_high_gt_low*STIM_linear*NPSpos + CUE_high_gt_low*STIM_quadratic*NPSpos + (CUE_high_gt_low*STIM*NPSpos|sub), data = demean_dropna)
sjPlot::tab_model(model.npsoutcome,
                  title = "Multilevel-modeling: \nlmer(OUTCOME_demean ~ CUE * STIM * NPSpos + (CUE * STIM *NPSpos | sub), data = pvc)",
                  CSS = list(css.table = '+font-size: 12;'))
Multilevel-modeling: lmer(OUTCOME_demean ~ CUE * STIM * NPSpos + (CUE * STIM *NPSpos | sub), data = pvc)
  OUTCOME_demean
Predictors Estimates CI p
(Intercept) -1.11 -1.88 – -0.34 0.005
CUE high gt low 9.11 6.99 – 11.23 <0.001
STIM linear 30.27 27.04 – 33.50 <0.001
NPSpos 0.18 0.10 – 0.25 <0.001
STIM quadratic 1.00 -0.58 – 2.58 0.217
CUE high gt low * STIM
linear 		-3.05 -6.76 – 0.66 0.107
CUE high gt low * NPSpos -0.09 -0.24 – 0.05 0.202
STIM linear * NPSpos -0.25 -0.43 – -0.07 0.007
CUE high gt low * STIM
quadratic 		-3.96 -7.14 – -0.78 0.015
NPSpos * STIM quadratic -0.03 -0.18 – 0.11 0.654
(CUE high gt low * STIM
linear) * NPSpos 		0.21 -0.12 – 0.54 0.207
(CUE high gt low
NPSpos) STIM quadratic 		-0.05 -0.35 – 0.25 0.762
Random Effects
σ2 372.61
τ00 sub 46.33
τ11 sub.CUE_high_gt_low 84.44
τ11 sub.STIMlow 157.74
τ11 sub.STIMmed 43.82
τ11 sub.NPSpos 0.01
τ11 sub.CUE_high_gt_low:STIMlow 19.20
τ11 sub.CUE_high_gt_low:STIMmed 14.72
τ11 sub.CUE_high_gt_low:NPSpos 0.20
τ11 sub.STIMlow:NPSpos 0.03
τ11 sub.STIMmed:NPSpos 0.05
τ11 sub.CUE_high_gt_low:STIMlow:NPSpos 0.15
τ11 sub.CUE_high_gt_low:STIMmed:NPSpos 0.33
ρ01 -0.09
-0.99
-0.99
-0.97
0.48
0.34
0.60
0.10
0.10
-0.44
-0.68
N sub 96
Observations 4147
Marginal R2 / Conditional R2 0.305 / NA

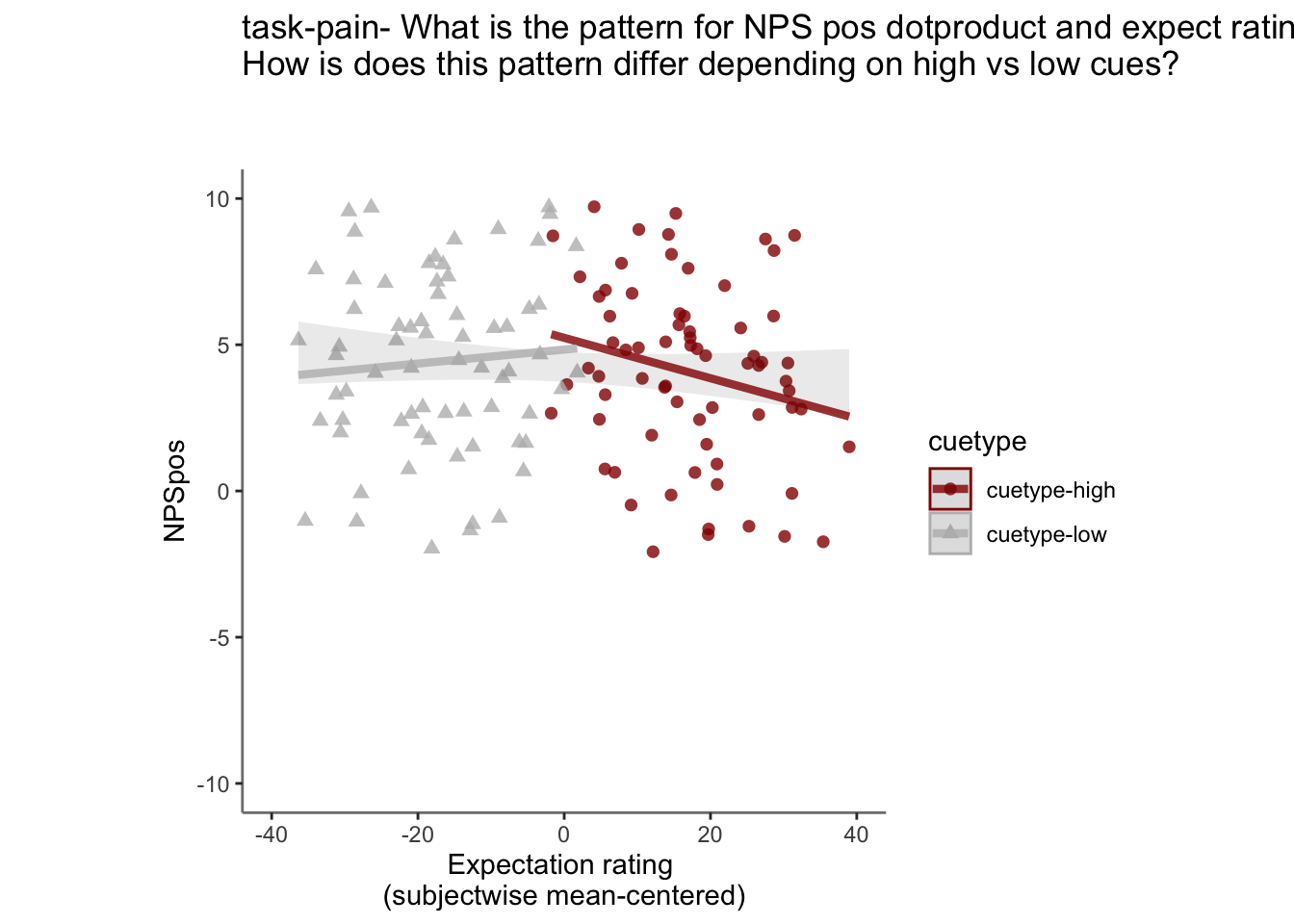
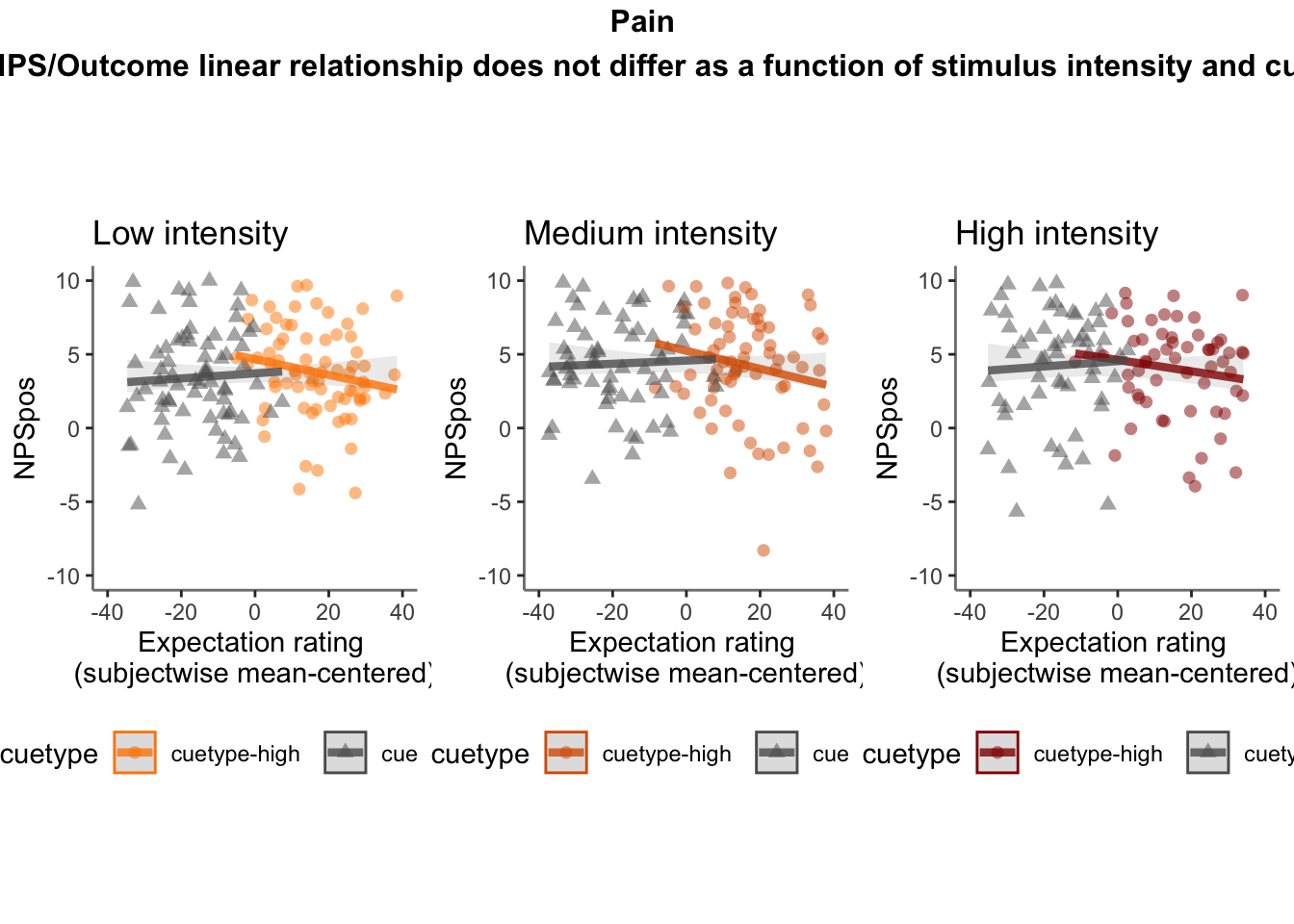
28.5 NPS ~ expectation_rating

Q. What is the relationship betweeen expectation ratings & NPS? (Pain task only)

Do we see a linear effect between expectation rating and NPS dot products? Also, does this effect differ as a function of cue and stimulus intensity ratings, as is the case for behavioral ratings?

Quick answer: Yes, expectation ratings predict NPS dotproducts; Also, there tends to be a different relationship depending on cues, just by looking at the figures, although this needs to be tested statistically.

28.5.1 demeaned expect rating * cue

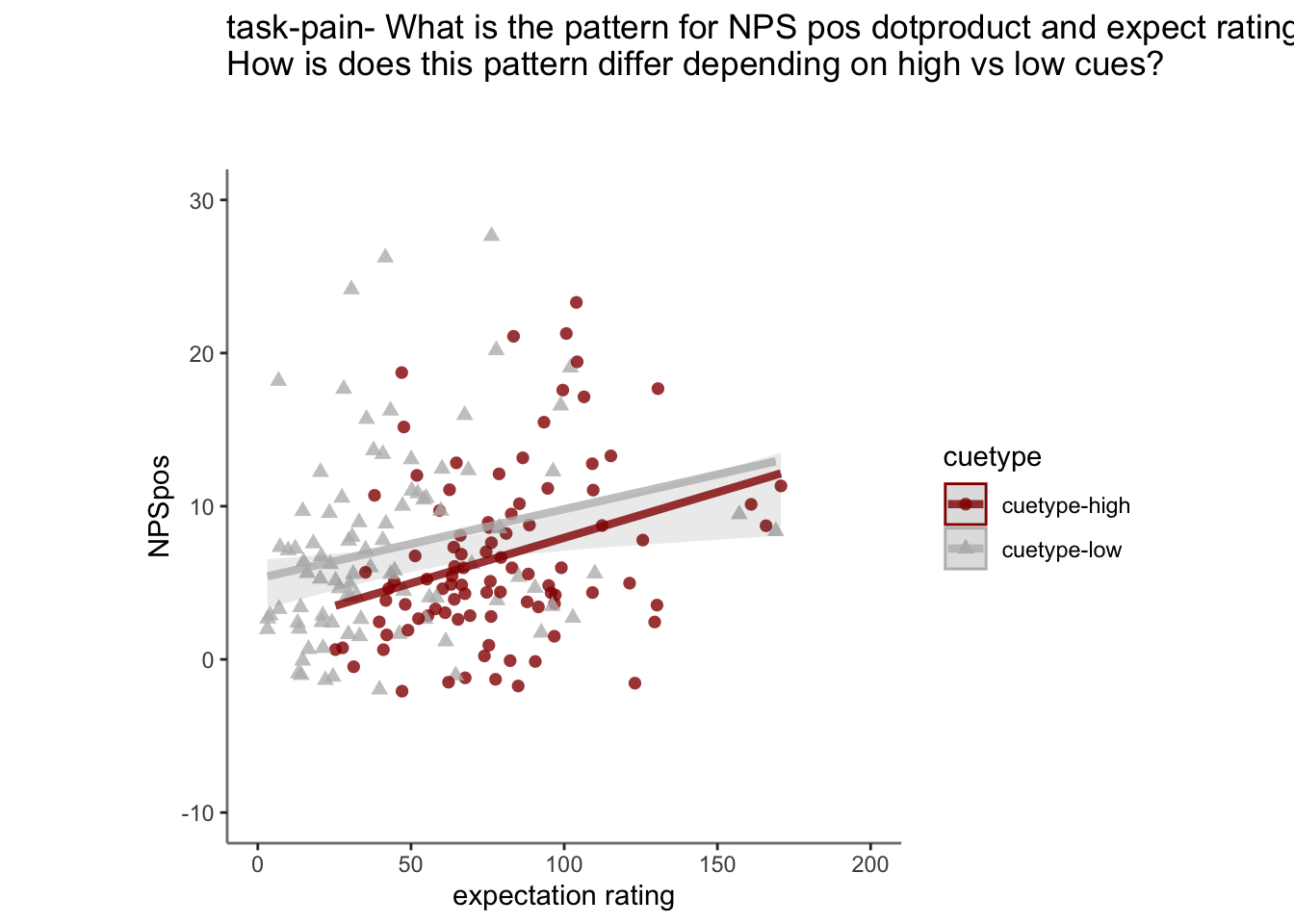
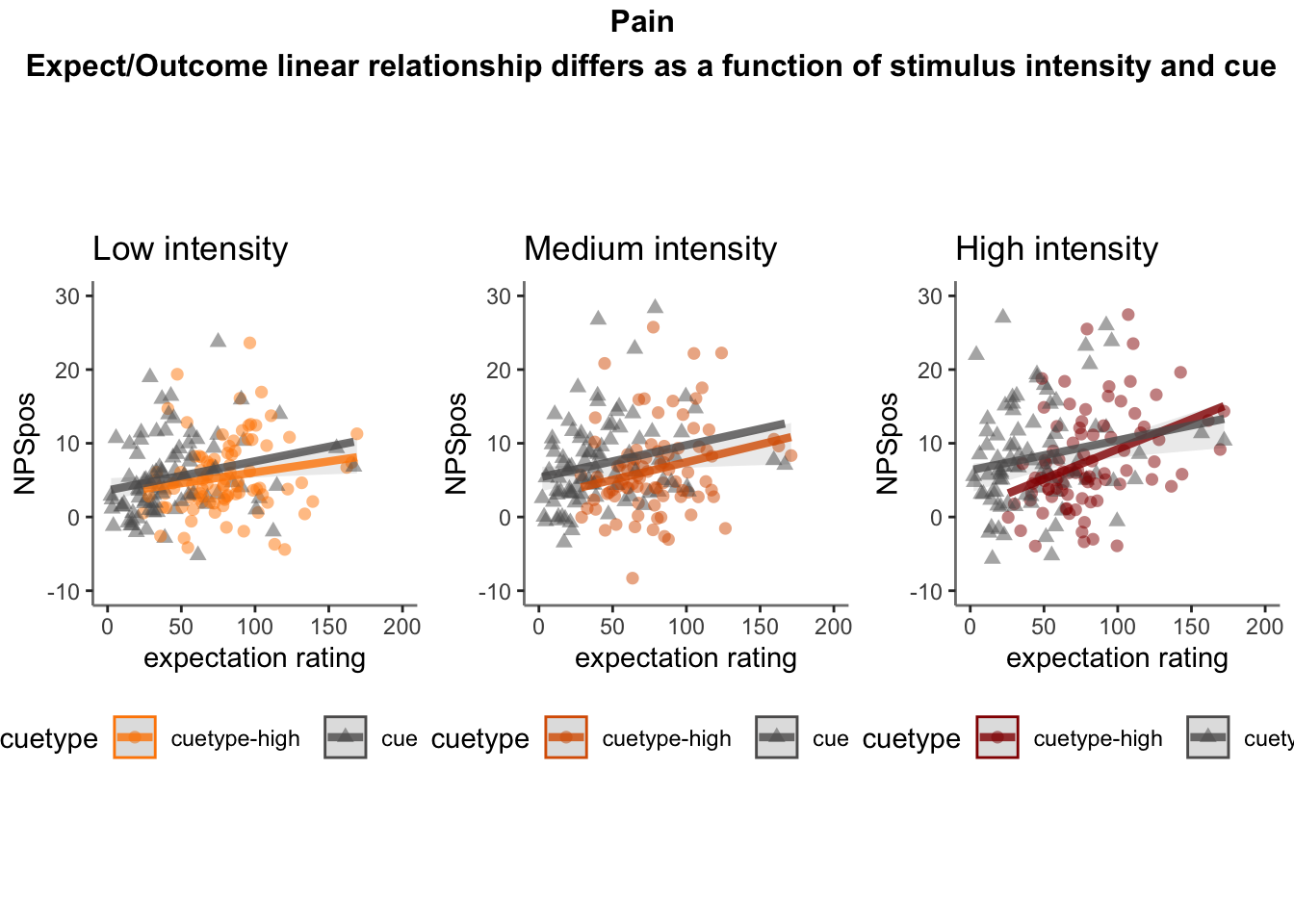
28.5.2 Is this statistically significant?

model.npsexpectdemean <- lmer(NPSpos ~ 
                          CUE_high_gt_low*STIM_linear*EXPECT_demean + 
                          CUE_high_gt_low*STIM_quadratic*EXPECT_demean + 
                          (CUE_high_gt_low+STIM+EXPECT_demean|sub), data = demean_dropna
                    )
sjPlot::tab_model(model.npsexpectdemean,
                  title = "Multilevel-modeling: \nlmer(NPSpos ~ CUE * STIM * EXPECT_demean + (CUE + STIM + EXPECT_demean| sub), data = pvc)",
                  CSS = list(css.table = '+font-size: 12;'))
Multilevel-modeling: lmer(NPSpos ~ CUE * STIM * EXPECT_demean + (CUE + STIM + EXPECT_demean| sub), data = pvc)
  NPSpos
Predictors Estimates CI p
(Intercept) 7.03 5.88 – 8.19 <0.001
CUE high gt low -0.55 -1.29 – 0.20 0.151
STIM linear 2.42 1.58 – 3.25 <0.001
EXPECT demean -0.00 -0.02 – 0.01 0.690
STIM quadratic -0.32 -1.01 – 0.36 0.357
CUE high gt low * STIM
linear 		-1.21 -2.73 – 0.30 0.117
CUE high gt low * EXPECT
demean 		-0.01 -0.04 – 0.01 0.314
STIM linear * EXPECT
demean 		0.01 -0.02 – 0.04 0.410
CUE high gt low * STIM
quadratic 		0.04 -1.30 – 1.37 0.956
EXPECT demean * STIM
quadratic 		-0.02 -0.04 – 0.00 0.112
(CUE high gt low * STIM
linear) * EXPECT demean 		0.02 -0.04 – 0.07 0.548
(CUE high gt low * EXPECT
demean) * STIM quadratic 		0.04 -0.01 – 0.09 0.121
Random Effects
σ2 61.71
τ00 sub 39.25
τ11 sub.CUE_high_gt_low 3.84
τ11 sub.STIMlow 2.92
τ11 sub.STIMmed 1.92
τ11 sub.EXPECT_demean 0.00
ρ01 -0.89
-0.91
-0.71
0.96
ICC 0.39
N sub 96
Observations 4004
Marginal R2 / Conditional R2 0.013 / 0.402 
demean_dropna$EXPECT <- demean_dropna$event02_expect_angle
model.npsexpect <- lmer(NPSpos ~ 
                          CUE_high_gt_low*STIM_linear*EXPECT + 
                          CUE_high_gt_low*STIM_quadratic*EXPECT + 
                          (CUE_high_gt_low+STIM+EXPECT|sub), data = demean_dropna
                    )
sjPlot::tab_model(model.npsexpect,
                  title = "Multilevel-modeling: \nlmer(NPSpos ~ CUE * STIM * EXPECT + (CUE + STIM + EXPECT| sub), data = pvc)",
                  CSS = list(css.table = '+font-size: 12;'))
Multilevel-modeling: lmer(NPSpos ~ CUE * STIM * EXPECT + (CUE + STIM + EXPECT| sub), data = pvc)
  NPSpos
Predictors Estimates CI p
(Intercept) 6.55 5.50 – 7.59 <0.001
CUE high gt low -0.62 -1.81 – 0.57 0.305
STIM linear 1.63 0.34 – 2.93 0.014
EXPECT 0.00 -0.01 – 0.02 0.685
STIM quadratic 0.63 -0.47 – 1.74 0.263
CUE high gt low * STIM
linear 		-2.19 -4.66 – 0.27 0.081
CUE high gt low * EXPECT -0.00 -0.02 – 0.01 0.835
STIM linear * EXPECT 0.01 -0.00 – 0.03 0.140
CUE high gt low * STIM
quadratic 		-1.34 -3.51 – 0.82 0.225
EXPECT * STIM quadratic -0.01 -0.03 – 0.00 0.102
(CUE high gt low * STIM
linear) * EXPECT 		0.02 -0.02 – 0.05 0.362
(CUE high gt low
EXPECT) STIM quadratic 		0.02 -0.01 – 0.05 0.217
Random Effects
σ2 61.69
τ00 sub 18.92
τ11 sub.CUE_high_gt_low 3.72
τ11 sub.STIMlow 2.53
τ11 sub.STIMmed 1.65
τ11 sub.EXPECT 0.00
ρ01 -0.86
-0.85
-0.54
0.81
N sub 96
Observations 4004
Marginal R2 / Conditional R2 0.022 / NA 
demean_dropna$EXPECT <- demean_dropna$event02_expect_angle
model.npsd_expectd <- lmer(NPS_demean ~ 
                          CUE_high_gt_low*STIM_linear*EXPECT_demean + 
                          CUE_high_gt_low*STIM_quadratic*EXPECT_demean + 
                          (CUE_high_gt_low+STIM+EXPECT_demean|sub), data = demean_dropna
                    )
## Warning: Model failed to converge with 2 negative eigenvalues: -2.7e+02 -1.1e+03
sjPlot::tab_model(model.npsd_expectd,
                  title = "Multilevel-modeling: \nlmer(NPS_demean ~ CUE * STIM * EXPECT_demean + (CUE + STIM + EXPECT_demean| sub), data = pvc)",
                  CSS = list(css.table = '+font-size: 12;'))
Multilevel-modeling: lmer(NPS_demean ~ CUE * STIM * EXPECT_demean + (CUE + STIM + EXPECT_demean| sub), data = pvc)
  NPS_demean
Predictors Estimates CI p
(Intercept) 0.15 -0.17 – 0.46 0.358
CUE high gt low -0.48 -1.24 – 0.28 0.216
STIM linear 2.39 1.63 – 3.14 <0.001
EXPECT demean -0.00 -0.02 – 0.01 0.692
STIM quadratic -0.27 -0.94 – 0.39 0.420
CUE high gt low * STIM
linear 		-1.01 -2.52 – 0.49 0.186
CUE high gt low * EXPECT
demean 		-0.01 -0.04 – 0.01 0.190
STIM linear * EXPECT
demean 		0.01 -0.02 – 0.04 0.513
CUE high gt low * STIM
quadratic 		-0.08 -1.41 – 1.24 0.904
EXPECT demean * STIM
quadratic 		-0.02 -0.04 – 0.01 0.134
(CUE high gt low * STIM
linear) * EXPECT demean 		0.02 -0.04 – 0.07 0.528
(CUE high gt low * EXPECT
demean) * STIM quadratic 		0.03 -0.02 – 0.08 0.188
Random Effects
σ2 60.84
τ00 sub 0.00
τ11 sub.CUE_high_gt_low 3.35
τ11 sub.STIMlow 0.02
τ11 sub.STIMmed 0.07
τ11 sub.EXPECT_demean 0.00
ρ01 -0.09
0.22
-0.41
-0.50
ICC 0.01
N sub 96
Observations 4004
Marginal R2 / Conditional R2 0.021 / 0.035